【题目】如图，
是
的直径，
切于点
，点
是上的一个动点（点不与
两点重合），连接
，过点
作
交于点
，过点作
于点
，交
的延长线于点
，连接
，
．
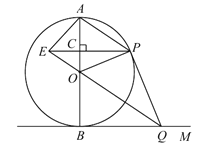
（1）求证：
．
（2）若直径的长为12．
①当
________时，四边形
为正方形；
②当________时，四边形
为菱形．
备战中考寒假系列答案科目：初中数学 来源： 题型：
【题目】某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，井建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数P=
（0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：Q=
（1）当8＜t≤24时，求P关于t的函数解析式；
（2）设第t个月销售该原料药的月毛利润为w（单位：万元）
①求w关于t的函数解析式；
②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P的最小值和最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
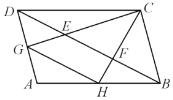
【题目】如图，
，
是平行四边形
从对角线
上的两点，
，连接
并延长交
于点
，连接
并延长交
于点
，连接
，设
的面积为
，
的面积为
，则与的关系正确的是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
内接于
，
是直径，点
在上，
，过点作
，垂足为
，连接
交
边于点
．
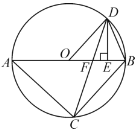
（1）求证：
；
（2）求证：
；
（3）连接
，设
的面积为
，
，求四边形
的面积（用含有的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.为了解一批灯泡的使用寿命，宜采用普查方式
B.掷两枚质地均匀的硬币，两枚硬币都是正面朝上这一事件发生的概率为
C.掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件
D.甲乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是S甲2＝0.4，S乙2＝0.6，则甲的射击成绩较稳定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，∠CAF＝2∠B．
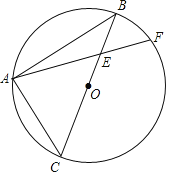
（1）求证：AE＝AC；
（2）若⊙O的半径为4，E是OB的中点，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
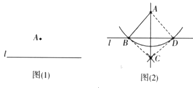
【题目】尺规作图：过直线外一点作已知直线的垂线，已知：如图（1），直线
及外一点
，求作的垂线，使它经过点，小红的做法如下：
①在直线上任取一点B，连接
②以为圆心，长为半径作弧，交直线于点
；
③分别以
为圆心， 长为半径作弧，两弧相交于点
；
④作直线
，直线即为所求如图（2），小红的做题依据是（ ）
A.四条边都相等的四边形是菱形；菱形的对角线互相垂直
B.直径所对的圆周角是直角
C.直线外一点到这条直线上垂线段最短
D.同圆或等圆中半径相等
查看答案和解析>>
科目：初中数学 来源： 题型：
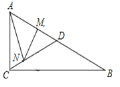
【题目】如图，在
中，
，
是
的中点，
，动点
从点
出发沿向终点
运动，动点
从点出发沿折线
向终点运动，两点速度均为每秒1个单位，两点同时出发，当其中一点到达终点后，运动停止，设运动时间为
，
的面积为
（平方单位），则与
之间的图象大致为（ ）
A.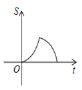
B.
C.
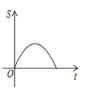D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
