
【题目】已知数轴上的A、B两点所对应的数分别为a、b.P为数轴上的一个动点.其中a,b满足(a﹣1)2+|b+5|=0,
(1)若点P为AB的中点,求P点对应的数.
(2)若点P从A点出发,以每秒2个单位的速度向左运动,t秒后,求P点所对应的数以及PB的距离.
(3)若数轴上点M、N所对应的数为m、n,其中A为PM的中点,B为PN的中点,无论点P在何处,![]() 是否为一个定值?若是,求出定值:若不是,请说明理由.
是否为一个定值?若是,求出定值:若不是,请说明理由.
【答案】(1)-2;(2)P点表示1﹣2t, PB=|6﹣2t|;(3)![]() 是一个定值,定值为2.
是一个定值,定值为2.
【解析】
(1)先确定a、b定值,由数轴上数中点的特点,求出P点的对应数;
(2)由题意可知,P点t秒后运动距离2t,P点表示1﹣2t,即可求PB;
(3)设P点表示的数为x,由两个中点,可知x=2﹣m,x=﹣10﹣n,求得m﹣n=12,即MN=|m﹣n|=12,所以![]() =
=![]() =2.
=2.
解:(1)由(a﹣1)2+|b+5|=0,
∴a=1,b=﹣5,
∴AB=6,
∵点P为AB的中点,
∴P点对应为﹣2;
(2)P点t秒后运动距离2t,
∴P点表示1﹣2t,
PB=|1﹣2t+5|=|6﹣2t|;
(3)设P点表示的数为x,
∵A为PM的中点,
∴x=2﹣m,
∵B为PN的中点,
∴x=﹣10﹣n,
∴2﹣m=﹣10﹣n,
∴m﹣n=12,
∵MN=|m﹣n|=12,
∴![]() =
=![]() =2,
=2,
∴![]() 是一个定值,定值为2.
是一个定值,定值为2.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
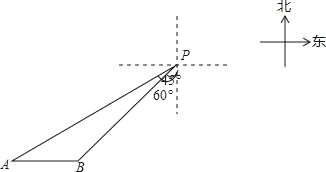
【题目】一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
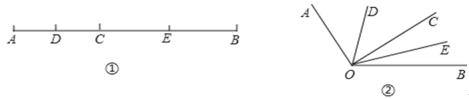
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,小慧同学利用直尺和规进行了如下操作:①连接AC,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
(1)线段AF与CF的数量关系是 .
(2)若∠BAD=120°,AE平分∠BAD,AB=8,求四边形AECF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1.例:[0.5]=﹣0.5.
(1)求[![]() ]、[﹣1]的值;
]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b],试求代数式(b﹣a)3﹣3a+3b的值;
(3)解方程:[x]+[x+2]=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两名选手参加长跑比赛,乙从起点出发匀速跑到终点,甲先快后慢,半个小时后找到适合自己的速度,匀速跑到终点,他们所跑的路程y(单位:km)随时间x(单位:h)变化的图象,如图所示,则下列结论错误的是( )
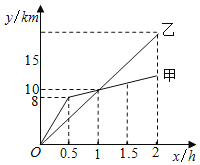
A. 在起跑后1h内,甲在乙的前面
B. 跑到1h时甲乙的路程都为10km
C. 甲在第1.5时的路程为11km
D. 乙在第2h时的路程为20km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com