
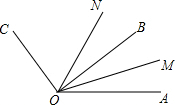
 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
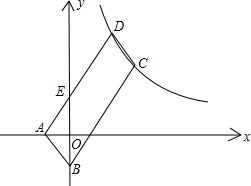 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-2),顶点C、D在双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
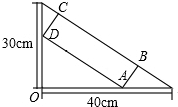 在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题:
如图所示为六月份某水库的水位图.由于从5号连续降雨,7号到达警戒水位20m,于是从7号开始开闸泻洪,并加固加高堤坝,10号到达30m的危险水位时停止了下雨,水位开始回落.请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
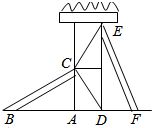 如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )
如图,有两个长度相等的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向上的长度DF相等,若∠ABC=32°,则∠DFE的度数为( )| A、32° | B、28° |
| C、58° | D、45° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| b-5 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com