
【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m.经测量,得到其它数据如图所示.其中∠CAH=37°,∠DBH=67°,AB=10m,请你根据以上数据计算GH的长.(参考数据tan67°![]() , tan37°
, tan37°![]() )
)
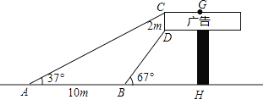
【答案】GH的长为10m.
【解析】
延长CD交AH于点E,则CE⊥AH,设DE=xm,则CE=(x+2)m,通过解直角三角形可得出AE=![]() ,BE=
,BE=![]() ,结合AE-BE=10可得出关于x的方程,解之即可得出x的值,再将其代入GH=CE=CD+DE中即可求出结论.
,结合AE-BE=10可得出关于x的方程,解之即可得出x的值,再将其代入GH=CE=CD+DE中即可求出结论.
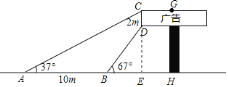
解:延长CD交AH于点E,则CE⊥AH,如图所示.
设DE=xm,则CE=(x+2)m,
在Rt△AEC和Rt△BED中,tan37°=![]() ,tan67°=
,tan67°=![]() ,
,
∴AE=![]() ,BE=
,BE=![]() .
.
∵AE﹣BE=AB,tan67°![]() , tan37°
, tan37°![]()
∴![]() ﹣
﹣![]() =10,
=10,
即![]() ﹣
﹣![]() =10,解得:x=8,
=10,解得:x=8,
∴DE=8m,
∴GH=CE=CD+DE=2m+8m=10m.
答:GH的长为10m.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】设函数y=x2+2kx+k﹣1(k为常数),下列说法正确的个数是( )
(1)对任意实数k,函数与x轴有两个交点
(2)当x≥﹣k时,函数y的值都随x的增大而增大
(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上
(4)对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上,延长
上,延长![]() 交
交![]() 于点
于点![]() .
.
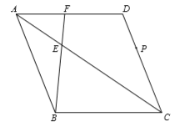
(1)求证:![]() ;
;
(2)已知点![]() 在边
在边![]() 上,请以
上,请以![]() 为边,用尺规作一个
为边,用尺规作一个![]() 与
与![]() 相似,并使得点
相似,并使得点![]() 在
在![]() 上.(只须作出一个
上.(只须作出一个![]() ,保留作图痕迹,不写作法)
,保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
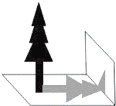
A.4.25mB.4.45mC.4.60mD.4.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.

(1)求剩余木料的面积.
(2)如果木工想从剩余的木料中截出长为1.5dm,宽为ldm的长方形木条,最多能截出 块这样的木条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2﹣4x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.
(1)若点P(﹣1,2)在图象G上,求n的值.
(2)当n=﹣1时.
①若Q(t,1)在图象G上,求t的值.
②当k≤x≤3(k<3)时,图象G对应函数的最大值为5,最小值为﹣5,直接写出k的取值范围.
(3)当以A(﹣3,3)、B(﹣3,﹣1)、C(2,﹣1)、D(2,3)为顶点的矩形ABCD的边与图象G有且只有三个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
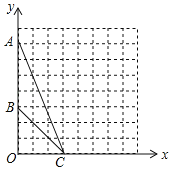
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
(1)在图中作出△ABC的外接圆(利用格图确定圆心);
(2)圆心坐标为 ;外接圆半径r为 ;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司根据市场需求销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划用不超过9.8万元购进A,B两种型号的净水器共50台,其中A型、B型净水器每台售价分别为2500元、2180元,设A型净水器为x台.
①求x的取值范围.
②若公司决定从销售A型净水器的利润中每台捐献a(100<a<150)元给贫困村饮水改造爱心工程,求售完这50台净水器后获得的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com