
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() гыyжсЯрНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxе§АыжсЯрНЛгкЕуBЃЌЖдГЦжсЪЧжБЯпx=1ЃЎ
гыyжсЯрНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxе§АыжсЯрНЛгкЕуBЃЌЖдГЦжсЪЧжБЯпx=1ЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНвдМАЕуBЕФзјБъЃЎ
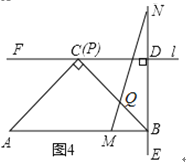
ЃЈ2ЃЉЖЏЕуMДгЕуOГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђдЫЖЏЃЌЭЌЪБЖЏЕуNДгЕуOГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиyжсе§ЗНЯђдЫЖЏЃЌЕБNЕуЕНДяAЕуЪБЃЌMЁЂNЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЖЏЕуMзїxжсЕФДЙЯпНЛЯпЖЮABгкЕуQЃЌНЛХзЮяЯпгкЕуPЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌЫФБпаЮOMPNЮЊОиаЮЃЎ
ЂкЕБtЃО0ЪБЃЌЁїBOQФмЗёЮЊЕШбќШ§НЧаЮЃПШєФмЃЌЧѓГіtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
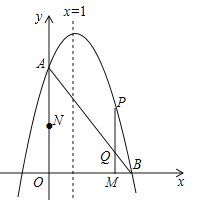
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ2ЃЉЂйЃЛЂкЃЎ
ЃЌBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛЃЈ2ЃЉЂйЃЛЂкЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЖдГЦжсЙЋЪНПЩЧѓЕУbЃЌгЩAЕузјБъПЩЧѓЕУcЃЌдђПЩЧѓЕУХзЮяЯпНтЮіЪНЃЛдйСюy=0ПЩЧѓЕУBЕузјБъЃЛ
ЃЈ2ЃЉЂйгУtПЩБэЪОГіONКЭOMЃЌдђПЩБэЪОГіPЕузјБъЃЌМДПЩБэЪОГіPMЕФГЄЃЌгЩОиаЮЕФаджЪПЩЕУON=PMЃЌПЩЕУЕНЙигкtЕФЗНГЬЃЌПЩЧѓЕУtЕФжЕЃЛЂкгЩЬтвтПЩжЊOB=OAЃЌЙЪЕБЁїBOQЮЊЕШбќШ§НЧаЮЪБЃЌжЛФмгаOB=BQЛђOQ=BQЃЌгУtПЩБэЪОГіQЕуЕФзјБъЃЌдђПЩБэЪОГіOQКЭBQЕФГЄЃЌЗжБ№ЕУЕНЙигкtЕФЗНГЬЃЌПЩЧѓЕУtЕФжЕЃЎ
ЃЈ1ЃЉЁпХзЮяЯп![]() ЖдГЦжсЪЧжБЯпx=1ЃЌ
ЖдГЦжсЪЧжБЯпx=1ЃЌ
ЁрЉ![]() =1ЃЌНтЕУb=2ЃЌ
=1ЃЌНтЕУb=2ЃЌ
ЁпХзЮяЯпЙ§AЃЈ0ЃЌ3ЃЉЃЌ
Ёрc=3ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЌСюy=0ПЩЕУ
ЃЌСюy=0ПЩЕУ![]() ЃЌНтЕУx=Љ1Лђx=3ЃЌ
ЃЌНтЕУx=Љ1Лђx=3ЃЌ
ЁрBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉЂйгЩЬтвтПЩжЊON=3tЃЌOM=2tЃЌ
ЁпPдкХзЮяЯпЩЯЃЌ
ЁрPЃЈ2tЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЫФБпаЮOMPNЮЊОиаЮЃЌ
ЁрON=PMЃЌ
Ёр3t=![]() ЃЌНтЕУt=1Лђt=Љ
ЃЌНтЕУt=1Лђt=Љ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕБtЕФжЕЮЊ1ЪБЃЌЫФБпаЮOMPNЮЊОиаЮЃЛ
ЂкЁпAЃЈ0ЃЌ3ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁрOA=OB=3ЃЌЧвПЩЧѓЕУжБЯпABНтЮіЪНЮЊy=Љx+3ЃЌ
ЁрЕБtЃО0ЪБЃЌOQЁйOBЃЌ
ЁрЕБЁїBOQЮЊЕШбќШ§НЧаЮЪБЃЌгаOB=QBЛђOQ=BQСНжжЧщПіЃЌгЩЬтвтПЩжЊOM=2tЃЌ
ЁрQЃЈ2tЃЌЉ2t+3ЃЉЃЌ
ЁрOQ=![]() ЃЌBQ=
ЃЌBQ=![]() |2tЉ3|ЃЌгжгЩЬтвтПЩжЊ0ЃМtЃМ1ЃЌЕБOB=QBЪБЃЌдђга
|2tЉ3|ЃЌгжгЩЬтвтПЩжЊ0ЃМtЃМ1ЃЌЕБOB=QBЪБЃЌдђга![]() |2tЉ3|=3ЃЌНтЕУt=
|2tЉ3|=3ЃЌНтЕУt=![]() ЃЈЩсШЅЃЉЛђt=
ЃЈЩсШЅЃЉЛђt=![]() ЃЛ
ЃЛ
ЕБOQ=BQЪБЃЌдђга![]() =
=![]() |2tЉ3|ЃЌНтЕУt=
|2tЉ3|ЃЌНтЕУt=![]() ЃЛ
ЃЛ
злЩЯПЩжЊЕБtЕФжЕЮЊ![]() Лђ
Лђ![]() ЪБЃЌЁїBOQЮЊЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїBOQЮЊЕШбќШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЃЉ
ШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЦНаагк
ЦНаагк![]() ЃЎ
ЃЎ![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯвЦЖЏЃЌНЧЕФвЛБп
ЩЯвЦЖЏЃЌНЧЕФвЛБп![]() ЪМжеОЙ§Еу
ЪМжеОЙ§Еу![]() ЃЌСэвЛБп
ЃЌСэвЛБп![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌбаОП
ЃЌбаОП![]() КЭ
КЭ![]() ЕФЪ§СПЙиЯЕЃЎ
ЕФЪ§СПЙиЯЕЃЎ
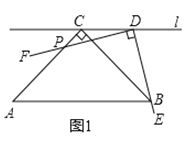
ЃЈЬНОПЗЂЯжЃЉ
ЃЈ1ЃЉШчЭМ2ЃЌФГЪ§бЇаЫШЄаЁзщдЫгУЁАДгЬиЪтЕНвЛАуЁБЕФЪ§бЇЫМЯыЃЌЗЂЯжЕБЕу![]() вЦЖЏЕНЪЙЕу
вЦЖЏЕНЪЙЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌЭЈЙ§ЭЦРэОЭПЩвдЕУЕН
жиКЯЪБЃЌЭЈЙ§ЭЦРэОЭПЩвдЕУЕН![]() ЃЌЧыаДГіжЄУїЙ§ГЬЃЛ
ЃЌЧыаДГіжЄУїЙ§ГЬЃЛ
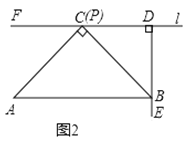
ЃЈЪ§бЇЫМПМЃЉ
ЃЈ2ЃЉШчЭМ3ЃЌШєЕу![]() ЪЧ
ЪЧ![]() ЩЯЕФШЮвтвЛЕуЃЈВЛКЌЖЫЕу
ЩЯЕФШЮвтвЛЕуЃЈВЛКЌЖЫЕу![]() ЃЉЃЌЪмЃЈ1ЃЉЕФЦєЗЂЃЌетИіаЁзщЙ§Еу
ЃЉЃЌЪмЃЈ1ЃЉЕФЦєЗЂЃЌетИіаЁзщЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌОЭПЩвджЄУї
ЃЌОЭПЩвджЄУї![]() ЃЌЧыЭъГЩжЄУїЙ§ГЬЃЛ
ЃЌЧыЭъГЩжЄУїЙ§ГЬЃЛ
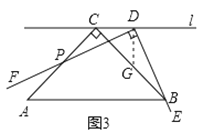
ЃЈЭиеЙв§ЩъЃЉ
ЃЈ3ЃЉШчЭМ4ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕу
БпЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕу![]() ЃЉЃЌ
ЃЉЃЌ![]() ЪЧЩфЯп
ЪЧЩфЯп![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌетИіЪ§бЇаЫШЄаЁзщОЙ§ЖрДЮШЁ
ЃЌетИіЪ§бЇаЫШЄаЁзщОЙ§ЖрДЮШЁ![]() ЕуЗДИДНјааЪЕбщЃЌЗЂЯжЕу
ЕуЗДИДНјааЪЕбщЃЌЗЂЯжЕу![]() дкФГвЛЮЛжУЪБ
дкФГвЛЮЛжУЪБ![]() ЕФжЕзюДѓЃЎШє
ЕФжЕзюДѓЃЎШє![]() ЃЌЧыФужБНгаДГі
ЃЌЧыФужБНгаДГі![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
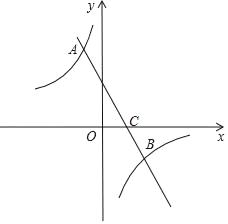
ЁОЬтФПЁПШчЭМЃЌжБЯпy=kx+bЃЈkЁй0ЃЉгыЫЋЧњЯпy=![]() ЃЈmЁй0ЃЉНЛгкЕуAЃЈЉ
ЃЈmЁй0ЃЉНЛгкЕуAЃЈЉ![]() ЃЌ2ЃЉЃЌBЃЈnЃЌЉ1ЃЉЃЎ
ЃЌ2ЃЉЃЌBЃЈnЃЌЉ1ЃЉЃЎ
ЃЈ1ЃЉЧѓжБЯпгыЫЋЧњЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЕуPдкxжсЩЯЃЌШчЙћSЁїABP=3ЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDЕФЫФИіЖЅЕуЖМдкЫЋЧњЯпyЃН![]() ЃЈkЃО0ЃЉЩЯЃЌBCЃН2ABЃЌЧвОиаЮABCDЕФУцЛ§ЪЧ32ЃЌдђkЕФжЕЪЧЃЈ ЃЉ
ЃЈkЃО0ЃЉЩЯЃЌBCЃН2ABЃЌЧвОиаЮABCDЕФУцЛ§ЪЧ32ЃЌдђkЕФжЕЪЧЃЈ ЃЉ
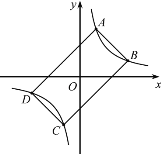
A.6B.8C.10D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
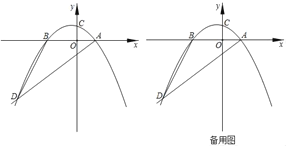
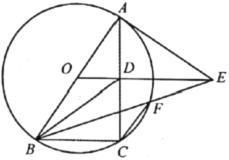
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉНЛxжсгкЕуAЃЈ2ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉЃЌНЛyжсгкЕуCЃЌЧвОЙ§ЕуdЃЈЉ6ЃЌЉ6ЃЉЃЌСЌНгADЃЌBDЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєЕуMЮЊXжсЩЯЗНЕФХзЮяЯпЩЯвЛЕуЃЌФмЗёдкЕуAзѓВрЕФxжсЩЯевЕНСэвЛЕуNЃЌЪЙЕУЁїAMNгыЁїABDЯрЫЦЃПШєЯрЫЦЃЌЧыЧѓГіДЫЪБЕуMЁЂЕуNЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуPЪЧжБЯпADЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгыAЃЌDжиКЯЃЉЃЌЙ§ЕуPзїPQЁЮyжсНЛжБЯпADгкЕуQЃЌвдPQЮЊжБОЖзїЁбEЃЌдђЁбEдкжБЯпADЩЯЫљНиЕУЕФЯпЖЮГЄЖШЕФзюДѓжЕЕШгкЁЁ ЁЁЃЎЃЈжБНгаДГіД№АИЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
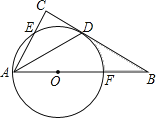
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌЁЯBACЕФЦНЗжЯпНЛBCгкЕуDЃЌЕуOдкABЩЯЃЌвдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЧЁКУОЙ§ЕуDЃЌЗжБ№НЛACЃЌABгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЪдХаЖЯжБЯпBCгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєBDЃН2![]() ЃЌBFЃН2ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ
ЃЌBFЃН2ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018ЮоЮ§ЪаЬхг§жаПМФаЩњЯюФПЗжЮЊЫйЖШФЭСІРрЁЂСІСПРрКЭСщЧЩРрЃЌУПЮЛПМЩњжЛФмдкШ§РржаИїбЁвЛЯюНјааПМЪдЃЎЦфжаЫйЖШФЭСІРрЯюФПгаЃК50УзХмЁЂ800УзХмЁЂ50УзгЮгОЃЛСІСПРрЯюФПгаЃКжРЪЕаФЧђЁЂв§ЬхЯђЩЯЃЛСщЧЩРрЯюФПгаЃК30УыжгЬјЩўЁЂСЂЖЈЬјдЖЁЂИЉЮдГХЁЂРКЧђдЫЧђЃЎФаЩњаЁУїЁА50УзХмЁБЪЧЧПЯюЃЌЫћОіЖЈБибЁЃЌЦфЫќЯюФПдкЦНЪБВтЪджаГЩМЈЭъШЋЯрЭЌЃЌЫћОіЖЈЫцЛњбЁдёЃЎ
ЃЈ1ЃЉЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓЁАаЁУїЁЎбЁ50УзХмЁЂв§ЬхЯђЩЯКЭСЂЖЈЬјдЖЁЏЁБЕФИХТЪЃЛ
ЃЈ2ЃЉаЁУїЫљбЁЕФЯюФПжагаСЂЖЈЬјдЖЕФИХТЪЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЪЧЯвЃЌЕу
ЪЧЯвЃЌЕу![]() дкдВЭтЃЌ
дкдВЭтЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЁЯA=30ЁуЃЌЕуPДгЕуAГіЗЂвд2cm/sЕФЫйЖШбиелЯпAЉCЉBдЫЖЏЃЌЕуQДгЕуAГіЗЂвдaЃЈcm/sЃЉЕФЫйЖШбиABдЫЖЏЃЌPЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБФГвЛЕудЫЖЏЕНЕуBЪБЃЌСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊxЃЈsЃЉЃЌЁїAPQЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЌyЙигкxЕФКЏЪ§ЭМЯѓгЩC1ЃЌC2СНЖЮзщГЩЃЌШчЭМ2ЫљЪОЃЎ
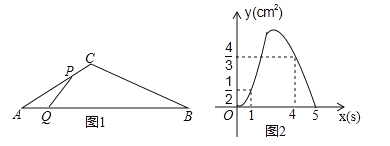
ЃЈ1ЃЉЧѓaЕФжЕЃЛ
ЃЈ2ЃЉЧѓЭМ2жаЭМЯѓC2ЖЮЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНЯпЖЮBCЩЯФГвЛЖЮЪБЁїAPQЕФУцЛ§ЃЌДѓгкЕБЕуPдкЯпЖЮACЩЯШЮвтвЛЕуЪБЁїAPQЕФУцЛ§ЃЌЧѓxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com