
ЎѕМвДїЎї![]() іЗУР·КБП
іЗУР·КБП![]() Ј¬
Ј¬![]() іЗУР·КБП
іЗУР·КБП![]() .ПЦТЄ°СХвР©·КБПИ«ІїФЛНщ
.ПЦТЄ°СХвР©·КБПИ«ІїФЛНщ![]() Ўў
Ўў![]() БЅПзЈ¬
БЅПзЈ¬![]() ПзРиТЄ·КБП240tЈ¬
ПзРиТЄ·КБП240tЈ¬![]() ПзРиТЄ·КБП
ПзРиТЄ·КБП![]() Ј¬ЖдФЛНщ
Ј¬ЖдФЛНщ![]() Ўў
Ўў![]() БЅПзµДФЛ·СИзПВ±нЈє
БЅПзµДФЛ·СИзПВ±нЈє
БЅіЗ/БЅПз | C/(ФЄ/ | D/(ФЄ/ |
| 20 | 24 |
| 15 | 17 |
ЙиґУ![]() іЗФЛНщ
іЗФЛНщ![]() ПзµД·КБПОЄ
ПзµД·КБПОЄ![]() Ј¬ґУ
Ј¬ґУ![]() іЗФЛНщБЅПзµДЧЬФЛ·СОЄ
іЗФЛНщБЅПзµДЧЬФЛ·СОЄ![]() ФЄЈ¬ґУ
ФЄЈ¬ґУ![]() іЗФЛНщБЅПзµДЧЬФЛ·СОЄ
іЗФЛНщБЅПзµДЧЬФЛ·СОЄ![]() ФЄ
ФЄ
(1)·Ц±рРґіц![]() Ўў
Ўў![]() Ул
Ул![]() Ц®јдµДєЇКэ№ШПµКЅ(І»ТЄЗуРґЧФ±дБїµДИЎЦµ·¶О§)Ј»
Ц®јдµДєЇКэ№ШПµКЅ(І»ТЄЗуРґЧФ±дБїµДИЎЦµ·¶О§)Ј»
(2)КФ±ИЅП![]() Ўў
Ўў![]() БЅіЗЧЬФЛ·СµДґуРЎЈ»
БЅіЗЧЬФЛ·СµДґуРЎЈ»
(3)Иф![]() іЗµДЧЬФЛ·СІ»µГі¬№э4800ФЄЈ¬ФхСщµчФЛК№БЅіЗЧЬ·СУГµДєНЧоЙЩ?ІўЗуіцЧоРЎЦµЈ®
іЗµДЧЬФЛ·СІ»µГі¬№э4800ФЄЈ¬ФхСщµчФЛК№БЅіЗЧЬ·СУГµДєНЧоЙЩ?ІўЗуіцЧоРЎЦµЈ®
Ўѕґр°ёЎї![]() Ј»(2) µ±
Ј»(2) µ±![]() К±Ј¬
К±Ј¬![]() Ј¬
Ј¬![]() іЗµДЧЬФЛ·СЅПЙЩЈ»µ±
іЗµДЧЬФЛ·СЅПЙЩЈ»µ±![]() К±Ј¬
К±Ј¬![]() Ј¬БЅіЗµДЧЬФЛ·СПаµИЈ»µ±
Ј¬БЅіЗµДЧЬФЛ·СПаµИЈ»µ±![]() К±Ј¬
К±Ј¬![]() Ј¬
Ј¬![]() іЗµДЧЬФЛ·СЅПЙЩЈ»ЈЁ3Ј©µ±
іЗµДЧЬФЛ·СЅПЙЩЈ»ЈЁ3Ј©µ±![]() К±Ј¬
К±Ј¬![]() УРЧоРЎЦµ
УРЧоРЎЦµ![]()
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭМвДїµДТЄЗуЈ¬AіЗФЛНщCПзµД·КБПОЄxtЈ¬ФтФЛНщDПзµД·КБПЈЁ200-xЈ©tЈ¬ґУBіЗФЛНщCПзµД·КБПОЄЈЁ240-xЈ©tЈ¬BіЗФЛНщDПзµД·КБПОЄЈЁx+60Ј©t,ґъИлјЖЛгїЙµГµЅЅб№ыЈ®
ЈЁ2Ј©УЙЈЁ1Ј©µГµЅµД![]() ЅшРР·ЦАаМЦВЫЈ¬·Ц±рКЗ
ЅшРР·ЦАаМЦВЫЈ¬·Ц±рКЗ![]() Ј¬јґїЙЗуіцЅб№ыЈ®
Ј¬јґїЙЗуіцЅб№ыЈ®
ЈЁ3Ј©ёщѕЭМвТвїЙБРіцІ»µИКЅ![]() Ј¬УГy±нКѕіцБЅіЗµДЧЬ·СУГЈ¬ХвСщѕНїЙТФёщѕЭєЇКэµДРФЦКЕР¶ПЈ®
Ј¬УГy±нКѕіцБЅіЗµДЧЬ·СУГЈ¬ХвСщѕНїЙТФёщѕЭєЇКэµДРФЦКЕР¶ПЈ®
(1)ТтОЄЙиґУAіЗФЛНщCПзµД·КБПОЄxtЈ¬ФтґУAіЗФЛНщDПз·ЁИЛ·КБПОЄ![]() Ј¬ґУBіЗФЛНщCПзµД·КБПОЄ
Ј¬ґУBіЗФЛНщCПзµД·КБПОЄ![]() Ј¬
Ј¬
ЎаґУBіЗФЛНщDПзµД·КБПОЄ![]()
Ўа![]() ,
,![]()
(2)УЙ![]() Ј¬ЅвµГ
Ј¬ЅвµГ![]() Ј¬
Ј¬
Ўаµ±![]() К±Ј¬
К±Ј¬![]() Ј¬
Ј¬![]() іЗµДЧЬФЛ·СЅПЙЩ
іЗµДЧЬФЛ·СЅПЙЩ
µ±![]() К±Ј¬
К±Ј¬![]() Ј¬БЅіЗµДЧЬФЛ·СПаµИЈ¬
Ј¬БЅіЗµДЧЬФЛ·СПаµИЈ¬
µ±![]() К±Ј¬
К±Ј¬![]() Ј¬
Ј¬![]() іЗµДЧЬФЛ·СЅПЙЩ
іЗµДЧЬФЛ·СЅПЙЩ
ЈЁ3Ј©УЙ![]() µГ
µГ![]() Ј¬
Ј¬
![]()
ЙиБЅіЗЧЬФЛ·СєНОЄ![]() Ј¬Фт
Ј¬Фт![]()
![]() Ј¬
Ј¬
Ўа![]() Лж
Лж![]() µДФцґу¶шјхРЎЈ¬
µДФцґу¶шјхРЎЈ¬
Ўаµ±![]() К±Ј¬
К±Ј¬![]() УРЧоРЎЦµ
УРЧоРЎЦµ![]()



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјўЕЈ¬ФЪЎчABCЦРЈ¬ЎПC=90ЎгЈ¬AC=8cmЈ¬BC=6cmЈ® µгMУЙµгBіц·ўСШBA·ЅПтПтµгAФИЛЩФЛ¶ЇЈ¬Н¬К±µгNУЙµгAіц·ўСШAC·ЅПтПтµгCФИЛЩФЛ¶ЇЈ¬ЛьГЗµДЛЩ¶ИѕщОЄ2cm/s Ј®Б¬ЅУMNЈ¬ЙиФЛ¶ЇК±јдОЄt(s)©v0ЈјtЈј4©wЈ¬ЅвґрПВБРОКМвЈє
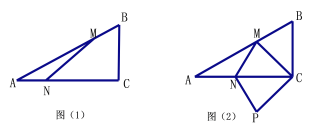
ўЕЙиЎчAMNµДГж»эОЄSЈ¬ЗуSУлtЦ®јдµДєЇКэ№ШПµКЅЈ¬ІўЗуіцSµДЧоґуЦµЈ»
ўЖИзНјўЖЈ¬Б¬ЅУMCЈ¬Ѕ«ЎчMNCСШNC·ХЫЈ¬µГµЅЛД±ЯРОMNPC,µ±ЛД±ЯРОMNPCОЄБвРОК±Ј¬ЗуtµДЦµЈ»
ўЗµ±tµДЦµОЄ Ј¬ЎчAMNКЗµИСьИэЅЗРОЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
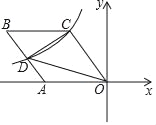
ЎѕМвДїЎїИзНјЈ¬БвРОOABCµДТ»±ЯOAФЪxЦбµДёє°лЦбЙПЈ¬OКЗЧш±кФµгЈ¬tanЎПAOC=![]() Ј¬·ґ±ИАэєЇКэy=©Ѓ
Ј¬·ґ±ИАэєЇКэy=©Ѓ![]() µДНјПуѕ№эµгCЈ¬УлABЅ»УлµгDЈ¬ФтЎчCODµДГж»эµДЦµµИУЪ_____Ј»
µДНјПуѕ№эµгCЈ¬УлABЅ»УлµгDЈ¬ФтЎчCODµДГж»эµДЦµµИУЪ_____Ј»
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
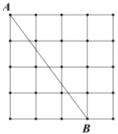
ЎѕМвДїЎїИзНјЈ¬µгAЈ¬BОЄ¶ЁµгЈ¬¶ЁЦ±ПЯl//ABЈ¬PКЗlЙПТ»¶ЇµгЈ®µгMЈ¬N·Ц±рОЄPAЈ¬PBµДЦРµгЈ¬¶ФУЪПВБРёчЦµЈє
ўЩПЯ¶ОMNµДі¤Ј»
ўЪЎчPABµДЦЬі¤Ј»
ўЫЎчPMNµДГж»эЈ»
ўЬЦ±ПЯMNЈ¬ABЦ®јдµДѕаАлЈ»
ўЭЎПAPBµДґуРЎЈ®
ЖдЦР»бЛжµгPµДТЖ¶Ї¶ш±д»ЇµДКЗЈЁ Ј©

A. ўЪўЫ B. ўЪўЭ C. ўЩўЫўЬ D. ўЬўЭ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Ѕ«ЎчABCИЖµгAДжК±ХлРэЧЄ60ЎгµГµЅЎчADEЈ¬Б¬ЅУCD.Иф![]() Ј¬Фт
Ј¬Фт![]() µДґуРЎКЗ___Ј®
µДґуРЎКЗ___Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛїјІйС§ЙъµДЧЫєПЛШЦКЈ¬ДіКРѕц¶ЁЈєѕЕДкј¶±ПТµЙъНіТ»ІОјУЦРїјКµСйІЩЧчїјКФЈ¬ёщѕЭЅсДкµДКµјКЗйїцЈ¬ЦРїјКµСйІЩЧчїјКФїЖДїОЄЈє![]() ЈЁОпАнЈ©Ўў
ЈЁОпАнЈ©Ўў![]() ЈЁ»ЇС§Ј©Ўў
ЈЁ»ЇС§Ј©Ўў![]() ЈЁЙъОпЈ©Ј¬ГїїЖКФМвёчОЄ
ЈЁЙъОпЈ©Ј¬ГїїЖКФМвёчОЄ![]() µАЈ¬їјЙъЛж»ъійИЎЖдЦР
µАЈ¬їјЙъЛж»ъійИЎЖдЦР![]() µАЅшРРїјКФЈ®РЎГчєНРЎАцКЗДіРЈѕЕДкј¶С§ЙъЈ¬РиІОјУКµСйїјКФЈ®
µАЅшРРїјКФЈ®РЎГчєНРЎАцКЗДіРЈѕЕДкј¶С§ЙъЈ¬РиІОјУКµСйїјКФЈ®
ЈЁ1Ј©РЎГчійµЅ»ЇС§КµСйµДёЕВКОЄ Ј»
ЈЁ2Ј©ИфЦ»ґУїјКФїЖДїїјВЗЈ¬РЎГчєНРЎАційµЅІ»Н¬їЖДїµДёЕВКОЄ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Нј![]() Хэ·ЅРОНшёсЈ¬ГїёцРЎХэ·ЅРОµД±Яі¤ОЄ1Ј¬Зл°ґТЄЗу»іцПВБРНјРОЈ¬Лщ»НјРОµДёчёц¶ҐµгѕщФЪЛщёшРЎХэ·ЅРОµД¶ҐµгЙПЈ®
Хэ·ЅРОНшёсЈ¬ГїёцРЎХэ·ЅРОµД±Яі¤ОЄ1Ј¬Зл°ґТЄЗу»іцПВБРНјРОЈ¬Лщ»НјРОµДёчёц¶ҐµгѕщФЪЛщёшРЎХэ·ЅРОµД¶ҐµгЙПЈ®
ЈЁ1Ј©ФЪНјЦР»іцТ»ёцЦ±ЅЗ![]() Ј¬ІўЗТЖдГж»эОЄ5Ј»
Ј¬ІўЗТЖдГж»эОЄ5Ј»
ЈЁ2Ј©ФЪНјЦР»іцТ»ёцµИСьЦ±ЅЗ![]() Ј»
Ј»
ЈЁ3Ј©Б¬ЅУ![]() Ј¬Ц±ЅУРґіц
Ј¬Ц±ЅУРґіц![]() µДі¤Ј®
µДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
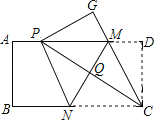
ЎѕМвДїЎїИзНјЈ¬ПИУРТ»ХЕѕШРОЦЅЖ¬![]() µг
µг![]() ·Ц±рФЪѕШРОµД±Я
·Ц±рФЪѕШРОµД±Я![]() ЙПЈ¬Ѕ«ѕШРОЦЅЖ¬СШЦ±ПЯMNХЫµюЈ¬К№µг
ЙПЈ¬Ѕ«ѕШРОЦЅЖ¬СШЦ±ПЯMNХЫµюЈ¬К№µг![]() ВдФЪѕШРОµД±Я
ВдФЪѕШРОµД±Я![]() ЙПЈ¬јЗОЄµг
ЙПЈ¬јЗОЄµг![]() Ј¬µг
Ј¬µг![]() ВдФЪ
ВдФЪ![]() ґ¦Ј¬Б¬ЅУ
ґ¦Ј¬Б¬ЅУ![]() Ј¬Ѕ»
Ј¬Ѕ»![]() УЪµг
УЪµг![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј®ПВБРЅбВЫЈє
Ј®ПВБРЅбВЫЈє
![]()
ўЪЛД±ЯРО![]() КЗБвРОЈ»
КЗБвРОЈ»
ўЫ![]() ЦШєПК±Ј¬
ЦШєПК±Ј¬![]() Ј»
Ј»
ўЬ![]() µДГж»э
µДГж»э![]() µДИЎЦµ·¶О§КЗ
µДИЎЦµ·¶О§КЗ![]()
ЖдЦРХэИ·µДКЗ_____ЈЁ°СХэИ·ЅбВЫµДРтєЕ¶јМоЙПЈ©Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї№ґ№Й¶ЁАнКЗИЛАаЧоО°ґуµДїЖС§·ўПЦЦ®Т»Ј¬ФЪОТ№ъ№ЕЛгКйЎ¶ЦЬчВЛгѕЎ·ЦРФзУРјЗФШЈ¬ИзНјўЩЈ¬ТФЦ±ЅЗИэЅЗРОµДёч±ЯОЄ±ЯПтНвЧчµИ±ЯИэЅЗРОЈ¬ФЩ°СЅПРЎµДБЅёцµИ±ЯИэЅЗРО°ґИзНјўЪµД·ЅКЅ·ЕЦГФЪЧоґуµИ±ЯИэЅЗРОДЪЈ®ИфЦЄµАНјўЪЦРТхУ°Ії·ЦµДГж»эЈ¬ФтТ»¶ЁДЬЗуіцНјўЪЦРЈЁ Ј©
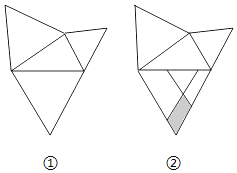
A.ЧоґуµИ±ЯИэЅЗРОУлЦ±ЅЗИэЅЗРОГж»эµДєНB.ЧоґуµИ±ЯИэЅЗРОµДГж»э
C.ЅПРЎБЅёцµИ±ЯИэЅЗРОЦШµюІї·ЦµДГж»эD.Ц±ЅЗИэЅЗРОµДГж»э
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com