
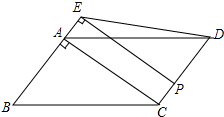
 如图,在?ABCD中,AB=3,BC=5,对角线AC⊥AB,点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度项终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连接PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).
如图,在?ABCD中,AB=3,BC=5,对角线AC⊥AB,点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度项终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连接PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).分析 (1)过点A作AF⊥BC,垂足为F,在三角形ABC中依据勾股定理可求得AC的长,然后依据三角形的面积公式可求得AF的长,从而得到AD与BC之间的距离;
(2)当0<t≤3时,如图2所示,先证明四边形AEPC是平行四边形,从而可知PE=AC=4;当3<t<8时,如图3所示;由题意可知PE∥AC,从而得到△BPE∽△BCA,由相似三角形的性质可知:$\frac{PE}{AC}=\frac{BP}{BC}$,从而可证得PE=$\frac{4(8-t)}{5}$=$-\frac{4}{5}t+\frac{32}{5}$;
(3)当0<t≤3时,如图4所示;设PE与AD的交点为F.由题意可知PF∥AC,从而得到△DPF∽△DCA,由相似三角形的性质可知$\frac{PF}{AC}=\frac{DP}{DC}$,从而可求得PF=$\frac{4t}{3}$,由三角形的面积公式可知S=$\frac{1}{2}DP•PF$=$\frac{2}{3}{t}^{2}$;当3<t<8时,如图5所示:延长DC、EP交于点G,则DG⊥EG.由证明△CPG∽△BCA,从而得到$\frac{CG}{AB}=\frac{PC}{BC}$,于是可求得DG=$\frac{3(t-3)}{5}$+3=$\frac{3t}{5}+\frac{6}{5}$,由三角形的面积公式可知:S=$\frac{1}{2}$PE•DG=-$\frac{6}{25}{t}^{2}+\frac{36}{25}t+\frac{96}{25}$.
解答 解:(1)如图1所示:过点A作AF⊥BC,垂足为F.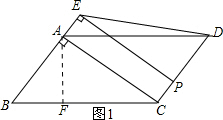
∵AC⊥AB,
∴∠BAC=90°.
在Rt△ABC中由勾股定理得:AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
∵${S}_{△ACB}=\frac{1}{2}AB•AC=\frac{1}{2}BC•AF$,
∴AF•BC=AB•AC,即5AF=12.
解得:AF=$\frac{12}{5}$.
∴AD与BC间的距离等于$\frac{12}{5}$.
故答案为:$\frac{12}{5}$.
(2)当0<t≤3时,如图2所示;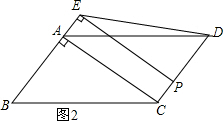
∵四边形ABCD是平行四边形,
∴AB∥CD.
∵PE⊥AB,AC⊥AB,
∴PE=AC=4.
当3<t<8时,如图3所示;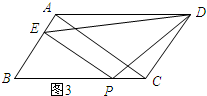
∵PE⊥AB,AC⊥AB,
∴PE∥AC.
∴△BPE∽△BCA.
∴$\frac{PE}{AC}=\frac{BP}{BC}$,即$\frac{PE}{4}=\frac{8-t}{5}$.
∴当PE=$\frac{4(8-t)}{5}$=$-\frac{4}{5}t+\frac{32}{5}$.
∴PE的长度=$\left\{\begin{array}{l}{4(0<t≤3)}\\{-\frac{4}{5}t+\frac{32}{5}(3<t<8)}\end{array}\right.$.
(3)当0<t≤3时,如图4所示;设PE与AD的交点为F.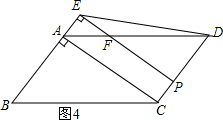
∵AC⊥AB,PE⊥AB,
∴PF∥AC.
∴△DPF∽△DCA.
∴$\frac{PF}{AC}=\frac{DP}{DC}$,即$\frac{PF}{4}=\frac{t}{3}$.
解得:PF=$\frac{4t}{3}$.
∴S=$\frac{1}{2}DP•PF$=$\frac{1}{2}×\frac{4}{3}t•t$=$\frac{2}{3}{t}^{2}$.
当3<t<8时,如图5所示:延长DC、EP交于点G,则DG⊥EG.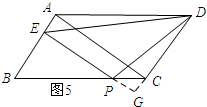
∵AB∥CD,
∴∠B=∠PCG.
∵∠BAC=∠PGC.
∴△CPG∽△BCA.
∴$\frac{CG}{AB}=\frac{PC}{BC}$,即$\frac{CG}{3}=\frac{t-3}{5}$.
∴OG=$\frac{3(t-3)}{5}$+3=$\frac{3t}{5}+\frac{6}{5}$.
∴S=$\frac{1}{2}$PE•DG=$\frac{1}{2}×(-\frac{4}{5}t+\frac{32}{5})(\frac{3}{5}t+\frac{6}{5})$=-$\frac{6}{25}{t}^{2}+\frac{36}{25}t+\frac{96}{25}$.
综上所述S与t的函数关系式为S=$\left\{\begin{array}{l}{\frac{2}{3}{t}^{2}(0<t≤3)}\\{-\frac{6}{25}{t}^{2}+\frac{36}{25}t+\frac{96}{25}(3<t<8)}\end{array}\right.$.
点评 本题主要考查的是相似三角形的综合应用,解答本题主要应用了相似三角形的性质和判定、平行四边形的性质和判定、勾股定理、三角形的面积公式,依据相似三角形的性质求得PE与DG的长度(用含t的式子表示)是解题的关键.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:选择题
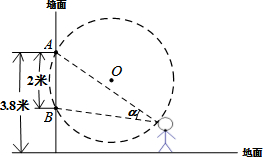 某学校为了提升学生素质,要求学生利用休息时间参加社会实践活动.四月的一个星期天,该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展.据展览说明介绍,参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳.当小慧看到一幅2米×2米的作品时(如图所示)发现该作品挂在墙面上的顶端A点距离地面3.8米.若小慧的眼睛距离地面1.60米,当看到该作品的效果达到最佳时,小慧的眼睛距离挂美术作品的墙面的最远距离是( )
某学校为了提升学生素质,要求学生利用休息时间参加社会实践活动.四月的一个星期天,该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展.据展览说明介绍,参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳.当小慧看到一幅2米×2米的作品时(如图所示)发现该作品挂在墙面上的顶端A点距离地面3.8米.若小慧的眼睛距离地面1.60米,当看到该作品的效果达到最佳时,小慧的眼睛距离挂美术作品的墙面的最远距离是( )| A. | 4米 | B. | 2$\sqrt{3}$米 | C. | (2+$\sqrt{3}$)米 | D. | ($\sqrt{3}$+1.6)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的运算程序中,若开始输入的x值为5,我们发现第1次输出的数为2,再将2输入,第2次输出的数为-1,如此循环,则第2015次输出的结果为-1.
如图所示的运算程序中,若开始输入的x值为5,我们发现第1次输出的数为2,再将2输入,第2次输出的数为-1,如此循环,则第2015次输出的结果为-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com