
【题目】如图,抛物线y=ax2+bx向上平移2个单位之后,正好与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
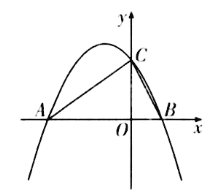
(1)求平移后抛物线的表达式;
(2)点Q是直线AC上方的抛物线上一点,过点Q作QE垂直于x轴,若以点B、Q、E为顶点的角形与△AOC相似,请求出Q点的坐标.
【答案】(1)![]() ;(2)Q(-2,2)或
;(2)Q(-2,2)或![]()
【解析】
(1)利用待定系数法求函数解析式;(2)如图所示,若以点B、Q、E为顶点的三角形与△AOC相似,有两种情况,需要分类讨论,不要漏解;
解:(1)∵抛物线y=ax2+bx向上平移2个单位
∴抛物线y=ax2+bx+2
又∵抛物线过点A(-3,0),B(1,0),
∴![]() ,
,
解得: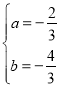 ,
,
∴二次函数的关系解析式为![]()
(2)如图所示,过点Q作QE垂直于x轴,设E(n,0),则BE=1-n,QE=![]()
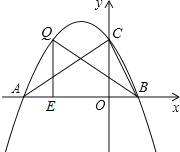
假设以点B、Q、E为顶点的三角形与△AOC相似,则有两种情况:
若△AOC∽△BEQ,则有:![]() ,
,
即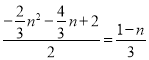 ,化简得:n2+n-2=0,
,化简得:n2+n-2=0,
解得n1=-2,n2=1(与B重合,舍去),
∴n=-2,QE=![]() =2
=2
∴Q(-2,2);
若△AOC∽△BQE,则有: ![]()
即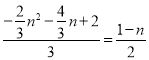 ,化简得:4n2-n-3=0,
,化简得:4n2-n-3=0,
解得n1=![]() ,n2=1(与B重合,舍去),
,n2=1(与B重合,舍去),
∴n=![]() ,QE=
,QE=![]() .
.
∴Q![]() .
.
综上所述,存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似.
Q点坐标为(-2,2)或![]()


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在圆![]() 中,直径
中,直径![]() ,
,![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() .
.
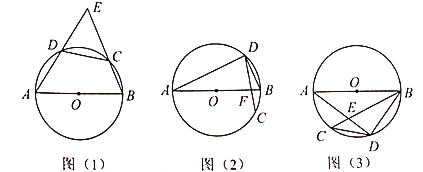
(1)求![]() 的度数;
的度数;
(2)如图2,![]() 与
与![]() 交于点
交于点![]() ,请补全图形并求
,请补全图形并求![]() 的度数;
的度数;
(3)如图3,弦![]() 与弦
与弦![]() 不相交,求
不相交,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨2元,月销售量就减少20kg,针对这种水产品情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备进一批每个进价为40元的小家电,经市场调查预测,售价定为50元时可售出400个;定价每增加1元,销售量将减少10个.
(1)设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)
(2)超市若准备获得利润6000元,并且使进货量较少,则每个应定价为多少元?
(3)超市若要获得最大利润,则每个应定价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
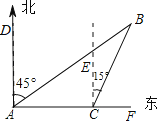
【题目】如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20![]() 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:
海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
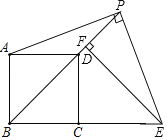
【题目】如图,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:①PA=PE;②CE=![]() PD;③BF﹣PD=
PD;③BF﹣PD=![]() BD;④S△PEF=S△ADP,正确的是___(填写所有正确结论的序号)
BD;④S△PEF=S△ADP,正确的是___(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
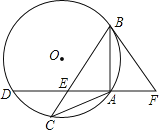
【题目】已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
(1)求证:BF与⊙O相切.
(2)若BF=5,cosC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com