
分析 (1)由已知各等式的规律可以总结得出$\frac{1}{42}$=$\frac{1}{6}$-$\frac{1}{7}$;
(2)由已知各等式的规律可以总结得出,再根据分式通分可以计算证明结论:$\frac{1}{m(m+1)}$=$\frac{1}{m}$-$\frac{1}{m+1}$;
(3)由(2)总结规律可以容易求出各式运算结果得零.
解答 解:(1)$\frac{1}{42}$=$\frac{1}{6×7}$=$\frac{1}{6}$-$\frac{1}{7}$
∴$\frac{1}{42}$=$\frac{1}{6}$-$\frac{1}{7}$
(2)猜想:$\frac{1}{m(m+1)}$=$\frac{1}{m}$-$\frac{1}{m+1}$.
理由如下:$\frac{1}{m}$-$\frac{1}{m+1}$=$\frac{m+1}{m(m+1)}$-$\frac{m}{m(m+1)}$=$\frac{m+1-m}{m(m+1)}$=$\frac{1}{m(m+1)}$
(3)原式=$\frac{1}{x-3}$-$\frac{1}{x-2}$-($\frac{1}{x-3}$-$\frac{1}{x-1}$)+$\frac{1}{x-2}$-$\frac{1}{x-1}$=0
点评 本题属于规律型题目,主要考察分式或分数的变形应用,可以很好的考察学生发现问题、总结问题、解决问题的能力.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
| A. | 3x2+4x-2=0 | B. | 2x2+5=6x | C. | 3x2-2$\sqrt{6}$x+2=0 | D. | 2x2+mx-1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,则∠ACB的度数为70°或110°.
如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,则∠ACB的度数为70°或110°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
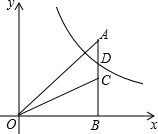 如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B,点C是线段AB上一点,函数y=$\frac{k}{x}$(k>0,x>0)的图象与线段AC交于点D(不与点A、C重合).若△AOB和△COB的面积分别为2和1,则k的值可能是( )
如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴于点B,点C是线段AB上一点,函数y=$\frac{k}{x}$(k>0,x>0)的图象与线段AC交于点D(不与点A、C重合).若△AOB和△COB的面积分别为2和1,则k的值可能是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
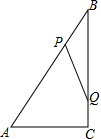 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com