
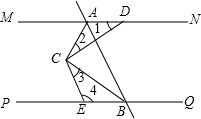
 如图,直线MN,PQ被直线AB所截,MN∥PQ,∠MAB与∠ABP的平分线交于点C,D是MN上的点,E是PQ上的点,连接CD,CE.
如图,直线MN,PQ被直线AB所截,MN∥PQ,∠MAB与∠ABP的平分线交于点C,D是MN上的点,E是PQ上的点,连接CD,CE.分析 (1)根据MN∥PQ得到∠MAB+∠ABP=180°,从而有$\frac{1}{2}$∠MAB+$\frac{1}{2}$∠ABP=$\frac{1}{2}$×180°=90°,即∠CAB+∠CBA=90°,可得AC⊥BC;
(2)将∠3+∠4-∠1-∠2转化为∠3+∠4-(∠1+∠2),最终转化为∠CAB+∠CBA=90°即可.
解答 解:(1)∵MN∥PQ,
∴∠MAB+∠ABP=180°,
∵∠MAB与∠ABP的平分线交于点C,
∴$\frac{1}{2}$∠MAB+$\frac{1}{2}$∠ABP=$\frac{1}{2}$×180°=90°,
∴∠CAB+∠CBA=90°,
∴AC⊥BC.
(2)∵∠1+∠2=∠MAC,∠3+∠4=∠CBQ,
∴∠3+∠4-∠1-∠2
=∠3+∠4-(∠1+∠2)
=∠CBQ-∠MAC
=∠MAB+∠CBA-∠MAC
=∠CAB+∠CBA
=90°.
点评 本题考查了平行线的性质,注意角度之间的转化,用整体思想求出角的度数.


科目:初中数学 来源: 题型:选择题
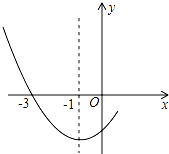 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),($\frac{5}{2}$,y2)是抛物线上两点,则y1>y2.其中说法正确的有( )个.
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),($\frac{5}{2}$,y2)是抛物线上两点,则y1>y2.其中说法正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
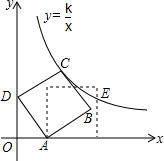 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}+1$ | C. | $\frac{1}{2}\sqrt{3}+1$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
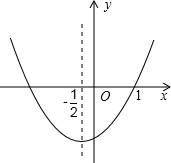 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-$\frac{1}{2}$,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-$\frac{1}{2}$,有下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
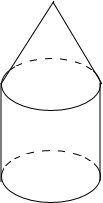 如图,用铁片做成一个上部为圆锥,下部为圆柱的无底活动房外壳,如果圆锥、圆柱的高分别为2米和3米,底面直径为4米,估计一下,做成这个活动房外壳至少需要多少铁皮?
如图,用铁片做成一个上部为圆锥,下部为圆柱的无底活动房外壳,如果圆锥、圆柱的高分别为2米和3米,底面直径为4米,估计一下,做成这个活动房外壳至少需要多少铁皮?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
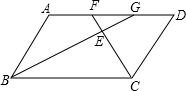 如图所示,四边形ABCD是平行四边形,F、G是AD边上的两个点,FC平分∠BCD,GB平分∠ABC,FC与GB相交于点E,求证:AF=GD.
如图所示,四边形ABCD是平行四边形,F、G是AD边上的两个点,FC平分∠BCD,GB平分∠ABC,FC与GB相交于点E,求证:AF=GD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com