
 已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.
已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.  一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
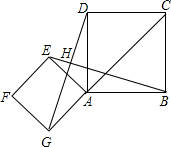 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
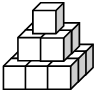 一个画家将14个边长为1m的正方形,他在地面上把它们摆成如图所示的形式,然后把露出表面的部分都涂上颜色,那么被涂上颜色的总面积的为33m2;若按此法摆放n层,那么露出表面的部分涂上颜色后的总面积可以表示为3n2+2n(m2).
一个画家将14个边长为1m的正方形,他在地面上把它们摆成如图所示的形式,然后把露出表面的部分都涂上颜色,那么被涂上颜色的总面积的为33m2;若按此法摆放n层,那么露出表面的部分涂上颜色后的总面积可以表示为3n2+2n(m2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
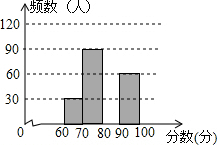 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com