
分析 利用因式分解法解方程易得x1=-$\frac{1}{3}$,x2=$\frac{m+1}{m-1}$,x=$\frac{m+1}{m-1}$为正整数,把x=$\frac{m+1}{m-1}$变形1+$\frac{2}{m-1}$,然后利用整数的整除性可确定m的值即可.
解答 解:3(m-1)x2-2(m+2)x-(m+1)=0
(3x+1)[(m-1)x-m-1]=0
解得x1=-$\frac{1}{3}$,x2=$\frac{m+1}{m-1}$,
∵关于x的二次方程3(m-1)x2-2(m+2)x-(m+1)=0有正整数根,
∴x=$\frac{m+1}{m-1}$=1+$\frac{2}{m-1}$为正整数,
∴m-1=1或2时,x=$\frac{2}{m-1}$为正整数,则m=2或3,
即所有满足条件的整数m的值为2或3.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).


科目:初中数学 来源: 题型:解答题
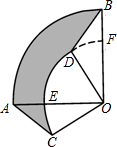 如图,把两个扇形OAB与扇形OCD的圆心重合叠放在一起,且∠AOB=∠COD,连接AC.
如图,把两个扇形OAB与扇形OCD的圆心重合叠放在一起,且∠AOB=∠COD,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
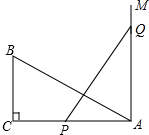 如图,Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.
如图,Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
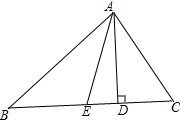 如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求:
如图,AD、AE分别是△ABC的高、中线,AB=15,BC=14,CA=13.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
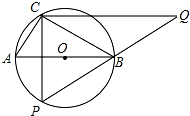 如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.
如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com