
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |


科目:初中数学 来源: 题型:
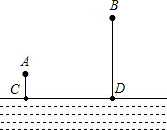 如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.
如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km.现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20 000元/千米.查看答案和解析>>
科目:初中数学 来源: 题型:
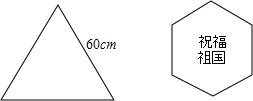 王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )
王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )| A、20cm | B、25cm |
| C、30cm | D、40cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com