
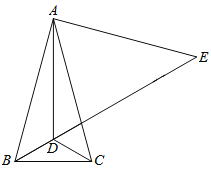
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
【答案】(1)60°;(2)见解析
【解析】试题分析:(1)△ABC中,AB=AC,∠BAC=30°,根据等腰三角形的性质和三角形的内角和定理可得∠ABC=∠ACB=75°,由DB=DC,∠DCB=30°,根据等腰三角形的性质再求得∠DBC=∠DCB=30°,即可得∠ABD=45°,易证AD所在直线垂直平分BC,根据等腰三角形的三线合一的性质可得AD平分∠BAC,即可求得∠BAD=15°,利用三角形外角的性质即可求得∠ADE=60°;(2)如图1,在线段DE上截取DM=AD,连接AM,证明△ABD≌△AEM,根据全等三角形的对应边相等和线段的和差即可证得结论.
试题解析:
(1)∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB=![]() =75°,∵DB=DC,∠DCB=30°,∴∠DBC=∠DCB=30°,
=75°,∵DB=DC,∠DCB=30°,∴∠DBC=∠DCB=30°,
∴∠ABD=∠ABC﹣∠DBC=45°,∵AB=AC,DB=DC,∴AD所在直线垂直平分BC,
∴AD平分∠BAC,∴∠BAD=![]() ∠BAC=15°,∴∠ADE=∠ABD+∠BAD=60°;
∠BAC=15°,∴∠ADE=∠ABD+∠BAD=60°;
(2)如图1,在线段DE上截取DM=AD,连接AM,
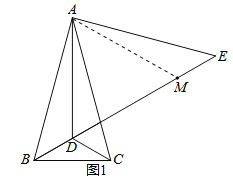
∵∠ADE=60°,DM=AD,
∴△ADM是等边三角形,∴∠ADB=∠AME=120°
∵AE=AB,∴∠ABD=∠E,
在△ABD和△AEM中,
∠ADB=∠AME,∠ABD=∠E,AB=AE,
∴△ABD≌△AEM(AAS),
∴BD=ME,∵BD=CD,∴CD=ME,
∵DE=DM+ME,∴DE=AD+CD.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线相等且互相平分
D.矩形的对角线互相垂直且平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据-2,-1,0, 6, 6, 20, 35,那么这组数据的中位数和众数分别是( )
A. 6和6 B. 3和6 C. 6和0 D. 9.5和6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.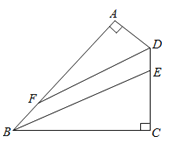
(1)若∠ABC=60°,则∠ADC= °,∠AFD=°;
(2)BE与DF平行吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市地铁2号线已开工,全长约332000m,将332000科学记数法表示应为( )
A. 0.332×106 B. 3.32×105 C. 33.2×104 D. 332×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2![]() ,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
(1)当△CEF成为等边三角形时,AE:EC= ;
(2)当EF=![]() 时,点D的坐标为 .
时,点D的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com