
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,A(1,0)、C(0,7).
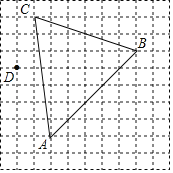
(1)在方格纸中画出平面直角坐标系,写出B点的坐标:B ;
(2)直接写出△ABC的形状: ,直接写出△ABC的面积 ;
(3)若D(﹣1,4),连接BD交AC于E,则![]() = .
= .
【答案】(1)如图,见解析;(6,5);(2)等腰三角形;20;(3)![]() .
.
【解析】
(1)利用A点和C点坐标画出x轴与y轴,然后写出B点坐标;
(2)根据勾股定理得到AC=![]() =5
=5![]() ,AB=
,AB=![]() =5
=5![]() ,求得△ABC是等腰三角形,根据三角形的面积=长方形的面积-3个三角形的面积即可得到结论;
,求得△ABC是等腰三角形,根据三角形的面积=长方形的面积-3个三角形的面积即可得到结论;
(3)设BD与y轴交于H,过B作BF⊥y轴于F,连接CD,根据勾股定理的逆定理得到∠DCB=90°,根据相似三角形的判定与性质即可得到结论.
(1)如图,建立如图所示的平面直角坐标系,
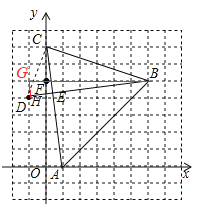
则B点的坐标为(6,5),
故答案为:(6,5);
(2)∵AC=![]() =5
=5![]() ,AB=
,AB=![]() =5
=5![]() ,
,
∴AC=AB,
∴△ABC是等腰三角形;
△ABC的面积=6×7﹣(![]() ×1×7+
×1×7+![]() ×2×6+
×2×6+![]() ×5×5)=20;
×5×5)=20;
故答案为:等腰三角形;20;
(3)设BD与y轴交于H,过B作BF⊥y轴于F,连接CD,
∵CD2=10,BC2=40,BD2=50,
∴CD2+BC2=BD2,
∴∠DCB=90°,
在△COA和△BGD中,
∴
∴△COA≌△BGD
∴∠ACO=∠DBF,∠DBF+∠BHF=90°,
∴∠ACO+∠BHF=90°
∴∠CEH=90°,
∴CE⊥BC,
在△DCE和△DBC中,
![]()
∴△DCE∽DBC
∴![]()
∴CD2=DEBD,
∴DE=![]() =
=![]() ,
,
∴BE=4![]() ,
,
∴![]() =
=![]() ,
,
故答案为:![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
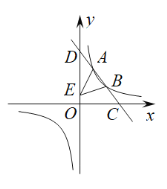
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种笔记本,进价为每本10元.试营销阶段发现:当销售单价为12元时,每天可卖出100本,如调整价格,每涨价1元,每天要少卖出10本.设该笔记本的销售单价为![]() 元,每天获得的销售利润为
元,每天获得的销售利润为![]() 元.
元.
(1)当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当![]() 时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
时,求销售单价为多少元时,该笔记本每天的销售利润最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度,方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN项部M的仰角为37°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E.请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan35°≈0.75)
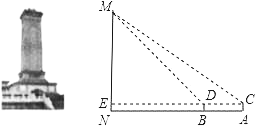
查看答案和解析>>
科目:初中数学 来源: 题型:
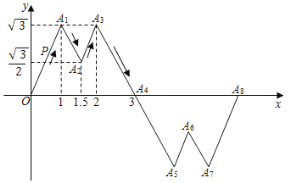
【题目】如图所示,A1(1,![]() ),A2(
),A2(![]() ,
,![]() ),A3(2,
),A3(2,![]() ),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
),A4(3,0).作折线A1A2A3A4关于点A4的中心对称图形,再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推,得到一个大的折线.现有一动点P从原点O出发,沿着折线一每秒1个单位的速度移动,设运动时间为t.当t=2020时,点P的坐标为( )
A.(1010,![]() )B.(2020,
)B.(2020,![]() )C.(2016,0)D.(1010,
)C.(2016,0)D.(1010,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
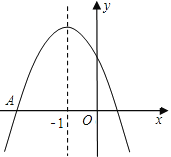
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
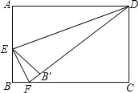
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进![]() 两种商品,已知购进
两种商品,已知购进![]() 种商品5件和
种商品5件和![]() 种商品4件共需300元;若购进
种商品4件共需300元;若购进![]() 种商品6件和
种商品6件和![]() 种商品8件共需440元;
种商品8件共需440元;
(1)求![]() 两种商品每件的进价分别为多少元?
两种商品每件的进价分别为多少元?
(2)若该商店,![]() 种商品每件的售价为48元,
种商品每件的售价为48元,![]() 种商品每件的售价为31元,且商店将购进
种商品每件的售价为31元,且商店将购进![]() 共50件的商品全部售出后,要获得的利润超过348元,求
共50件的商品全部售出后,要获得的利润超过348元,求![]() 种商品至少购进多少件?
种商品至少购进多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com