
【题目】已知二次函数y=![]() x2﹣x﹣
x2﹣x﹣![]() .
.
(1)在平面直角坐标系内,画出该二次函数的图象;
(2)根据图象写出:①当x 时,y>0;
②当0<x<4时,y的取值范围为 .
【答案】(1)见解析;(2)①x<﹣1或x>3;②﹣2≤y<![]() .
.
【解析】
(1)先把解析式配成顶点式得到抛物线的顶点坐标为(1,2);再分别求出抛物线与坐标轴的交点坐标,然后利用描点法画二次函数图象;
(2)①利用函数图象写出抛物线在x轴上方所对应的自变量的范围即可;
②先确定x=4时,y=![]() ,然后利用函数图象写出当0<x<4时对应的函数值的范围.
,然后利用函数图象写出当0<x<4时对应的函数值的范围.
解:(1)∵y=![]() (x﹣1)2﹣2,
(x﹣1)2﹣2,
∴抛物线的对称轴为直线x=1,顶点坐标为(1,2);
当x=0时,y=![]() x2﹣x﹣
x2﹣x﹣![]() =﹣
=﹣![]() ,则抛物线与y轴交点坐标为(0,﹣
,则抛物线与y轴交点坐标为(0,﹣![]() )
)
当y=0时,![]() x2﹣x﹣
x2﹣x﹣![]() =0,解得x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0)、(3,0),
=0,解得x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0)、(3,0),
如图,
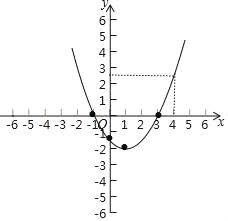
(2)①当x<﹣1或x>3时,y>0;
②当0<x<4时,﹣2≤y<![]() ;
;
故答案为x<﹣1或x>3;﹣2≤y<![]() .
.


科目:初中数学 来源: 题型:
【题目】某商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的售价p(元/千克)与时间t(天)之间的函数表达式为
p=
且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求第30天的日销售量是多少?
(2)问:哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3 000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.
(1)若商家将这批槟榔芋贮藏x天后一次性出售,请完成下列表格:
每千克槟榔芋售价 (单位:元) | 可供出售的槟榔芋重量 (单位:千克) | |
现在出售 | 3 000 | |
x天后出售 |
(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得总利润29 000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+3与y轴交于点A,与反比例函数y=![]() (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )

A. y=![]() B. y=-
B. y=-![]() C. y=
C. y=![]() D. y=-
D. y=-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB是⊙O的直径,![]() ,连接AC.
,连接AC.
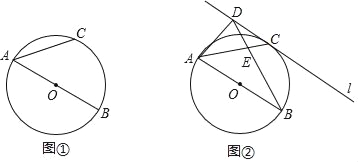
(1)求证:∠CAB=45°;
(2)如图②,直线l经过点C,在直线l上取一点D,使BD=AB,BD与AC相交于点E,连接AD,且AD=AE.
①求证:直线l是⊙O的切线;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com