
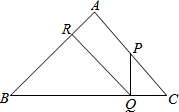
 如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.
如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.分析 (1)易得△ABC为等腰直角三角形,则∠B=∠C=45°,然后利用PQ⊥CQ可得到△PCQ为等腰直角三角形,所以PQ=CQ;
(2)根据等腰直角三角形的性质得BC=$\sqrt{2}$AB=$\sqrt{2}$,CQ=$\frac{\sqrt{2}}{2}$PC=$\frac{\sqrt{2}}{2}$x,同理可证得为△BQR等腰直角三角形,则BQ=$\sqrt{2}$RQ=$\sqrt{2}$y,所以$\sqrt{2}$y+$\frac{\sqrt{2}}{2}$x=1,变形得到y=-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$(0<x<1),然后描点画函数图象;
(3)由于AR=1-y,AP=1-x,则AR=1-(-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$),当AR=AP时,PR∥BC,所以1-(-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$)=1-x,解得x=$\sqrt{2}$,然后利用0<x<1可判断x=$\sqrt{2}$舍去,所以PR不能平行于BC.
解答 (1)证明:∵∠A=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∵PQ⊥CQ,
∴△PCQ为等腰直角三角形,
∴PQ=CQ;
(2)解:∵△ABC为等腰直角三角形,
∴BC=$\sqrt{2}$AB=$\sqrt{2}$,
∵△PCQ为等腰直角三角形,
∴CQ=$\frac{\sqrt{2}}{2}$PC=$\frac{\sqrt{2}}{2}$x,
同理可证得为△BQR等腰直角三角形,
∴BQ=$\sqrt{2}$RQ=$\sqrt{2}$y,
∵BQ+CQ=BC,
∴$\sqrt{2}$y+$\frac{\sqrt{2}}{2}$x=1,
∴y=-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$(0<x<1),
如图,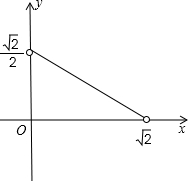
(3)解:不能.理由如下:
∵AR=1-y,AP=1-x,
∴AR=1-(-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$),
当AR=AP时,PR∥BC,
即1-(-$\frac{1}{2}$x+$\frac{\sqrt{2}}{2}$)=1-x,
解得x=$\sqrt{2}$,
∵0<x<1,
∴x=$\sqrt{2}$舍去,
∴PR不能平行于BC.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是熟练应用等腰直角三角形的性质.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.
如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
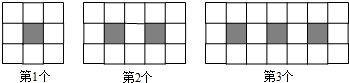
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com