
 等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°
等腰Rt△ABC和等腰Rt△ADE中,AB=AE,AD=AE,∠BAC=∠DAE=90°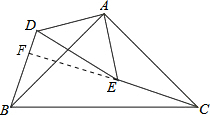 证明:(1)∵△ABC与△ADE都为等腰直角三角形,
证明:(1)∵△ABC与△ADE都为等腰直角三角形,
|


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
| A、(-x+y)(-x-y) |
| B、(a-2b)(2b+a) |
| C、(a-b)(a+b)(a2+b2) |
| D、(a+b-c)(a+b-c) |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 5 |
| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 序号 | 方程 | 方程的解 |
| 1 | x2-2x-3=0 | x1=-1,x2=3 |
| 2 | x2-4x-12=0 | x1=-2,x2=6 |
| 3 | x2-6x-27=0 | x1= |
查看答案和解析>>
科目:初中数学 来源: 题型:
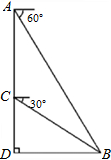 小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
小明运用所学的数学知识对某建筑物进行测量,测量方法如图所示:在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 9x2 |
| 5 |
| 6x |
| 3 |
| 4x2 |
| 4 |
| 2-a |
| x2-4y2 |
| x2+2xy+y2 |
| x+2y |
| x2+xy |
| a-b |
| a+2b |
| a2-b2 |
| a2+4ab+4b2 |
| 8 |
| x+1 |
| x+3 |
| x+1 |
| 2x2 |
| 3y2 |
| 5y |
| 6x |
| 10y |
| 21x2 |
| a2+b2 |
| a2-b2 |
| a-b |
| a+b |
| 2ab |
| (a-b)(a+b)2 |
| 1 |
| 4 |
| m2n2 |
| m2+2mn+n2 |
| 2 |
| mn |
| 1 |
| m |
| 1 |
| n |
| 1 |
| m-n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com