
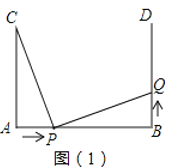
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由
(2)判断此时线段PC和线段PQ的关系,并说明理由。
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由。
【答案】(1)△ACP≌△BPQ,理由见解析;
(2)PC=PQ且PC⊥PQ,理由见解析;
(3)存在;![]() 或
或![]() .
.
【解析】
(1)利用SAS证得△ACP≌△BPQ;
(2)由(1)得出PC=PQ,∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(3)分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
解:(1)如图(1),△ACP≌△BPQ,理由如下:
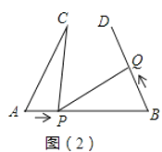
当t=1时,AP=BQ=1,
∴BP=AC=3,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
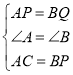 ,
,
∴△ACP≌△BPQ(SAS).
(2)PC=PQ且PC⊥PQ,理由如下:
由(1)可知△ACP≌△BPQ
∴PC=PQ,∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
∴PC⊥PQ.
(3)如图(2),分两种情况讨论:
当AC=BP,AP=BQ时,△ACP≌△BPQ,则
![]() ,
,
解得![]() ,
,
当AC=BQ,AP=BP时,△ACP≌△BQP,则,
![]()
解得![]()
综上所述,存在![]() 或
或![]() 使得△ACP与△BPQ全等.
使得△ACP与△BPQ全等.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图①所示,在三角形纸片![]() 中,
中,![]() ,
,![]() ,将纸片的一角折叠,使点
,将纸片的一角折叠,使点![]() 落在
落在![]() 内的点
内的点![]() 处.
处.
(1)若![]() ,
,![]() ________.
________.
(2)如图①,若各个角度不确定,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,直接写出结论.
之间的数量关系,直接写出结论.
②当点![]() 落在四边形
落在四边形![]() 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,
外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,![]() ,
,![]() ,
,![]() 之间又存在什么关系?请说明。
之间又存在什么关系?请说明。
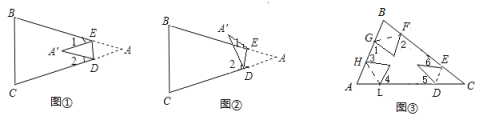
(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的![]() 和是________.
和是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
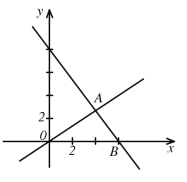
(1)求直线![]() 的函数关系式.
的函数关系式.
(2)求![]() 的面积.
的面积.
(3)是否存在点![]() ,使
,使![]() 的面积与
的面积与![]() 的面积相等?若存在求出此时点
的面积相等?若存在求出此时点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 件同型号的产品中,有
件同型号的产品中,有![]() 件不合格品和
件不合格品和![]() 件合格品
件合格品
![]() 从这
从这![]() 件产品中随即抽取
件产品中随即抽取![]() 件进行检测,列表或画树状图,求抽到都是合格品的概率.
件进行检测,列表或画树状图,求抽到都是合格品的概率.
![]() 在这
在这![]() 件产品中加入
件产品中加入![]() 件合格品后,进行如下试验:随即抽取
件合格品后,进行如下试验:随即抽取![]() 件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在
件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在![]() ,则可以推算出
,则可以推算出![]() 的值大约是多少?
的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是__________.(只需写出一个即可,图中不能再添加别的“点”和“线”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕着点B顺时针旋转角a(0°<a<90°)得到△A1BC;A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论.
(2)如图2,当a=30°时,试判断四边形BC1DA的形状,并证明.
(3)在(2)的条件下,求线段DE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com