


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 路程(千米) | 运费(元/吨.千米) | |||
| A仓库 | B仓库 | A仓库 | B仓库 | |
| 甲工地 | 20 | 25 | 0.8 | 1 |
| 乙工地 | 15 | 20 | 1.2 | 1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点O是AC上一点,OE,OF分别平分∠AOB,∠BOC.
如图,点O是AC上一点,OE,OF分别平分∠AOB,∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:
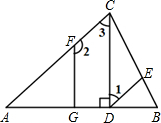 已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.
已知:在△ABC中,CD是AB边上的高,∠DEB=∠ACB,∠1+∠2=180°.试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com