
【题目】定义:当点C在线段AB上,AC=nAB时,我们称n为点C在线段AB上的点值,记作dC﹣AB=n.理解:如点C是AB的中点时,即AC=![]() AB,则dC﹣AB=
AB,则dC﹣AB=![]() ;反过来,当dC﹣AB=
;反过来,当dC﹣AB=![]() 时,则有AC=
时,则有AC=![]() AB.因此,我们可以这样理解:dC﹣AB=n与AC=nAB具有相同的含义.
AB.因此,我们可以这样理解:dC﹣AB=n与AC=nAB具有相同的含义.

应用:(1)如图1,点C在线段AB上,若dC﹣AB=![]() ,则AC= AB;若AC=3BC,则dC﹣AB= ;
,则AC= AB;若AC=3BC,则dC﹣AB= ;
(2)已知线段AB=10cm,点P、Q分别从点A和点B同时出发,相向而行,当点P到达点B时,点P、Q均停止运动,设运动时间为ts.
①若点P、Q的运动速度均为1cm/s,试用含t的式子表示dP﹣AB和dQ﹣AB,并判断它们的数量关系;
②若点P、Q的运动速度分别为1cm/s和2cm/s,点Q到达点A后立即以原速返回,则当t为何值时,dP﹣AB+dQ﹣AB=![]() ?
?
拓展:如图2,在三角形ABC中,AB=AC=12,BC=8,点P、Q同时从点A出发,点P沿线段AB匀速运动到点B,点Q沿线段AC,CB匀速运动至点B.且点P、Q同时到达点B,设dP﹣AB=n,当点Q运动到线段CB上时,请用含n的式子表示dQ﹣CB.
【答案】应用:(1)![]() ;
;![]() ;(2)①dP﹣AB=
;(2)①dP﹣AB=![]() ,dQ﹣AB=
,dQ﹣AB=![]() ,dP﹣AB+dQ﹣AB=1;②t=4或
,dP﹣AB+dQ﹣AB=1;②t=4或![]() ;拓展:dQ﹣CB=
;拓展:dQ﹣CB=![]() .
.
【解析】
应用:(1)根据dC﹣AB=n与AC=nAB具有相同的含义,进行解答即可;
(2)①用含t的式子先表示出AP,AQ,再由定义可求解;
②分t<5与t≥5两种情况,根据定义可得dP﹣AB=![]() ,dQ﹣AB=
,dQ﹣AB=![]() (t<5),dQ﹣AB=
(t<5),dQ﹣AB=![]() (t≥5),由dP﹣AB+dQ﹣AB=
(t≥5),由dP﹣AB+dQ﹣AB=![]() ,列出方程即可求解;
,列出方程即可求解;
拓展:设运动时间为t,由题意点P、Q同时到达点B,可设点P的速度为3x,点Q速度为5x,可得dP﹣AB=n=![]() ,dQ﹣CB=
,dQ﹣CB=![]() ,求解即可.
,求解即可.
解:应用:(1)∵dC﹣AB=![]() ,∴AC=
,∴AC=![]() AB,
AB,
∵AC=3BC,∴AC=![]() AB,∴dC﹣AB=
AB,∴dC﹣AB=![]() ,
,
故答案为:![]() ;
;![]() ;
;
(2)①∵点P、Q的运动速度均为1cm/s,
∴AP=tcm,AQ=(10﹣t)cm,
∴dP﹣AB=![]() ,dQ﹣AB=
,dQ﹣AB=![]() ,
,
∴dP﹣AB+dQ﹣AB=![]() =1;
=1;
②∵点P、Q的运动速度分别为1cm/s和2cm/s,
∴AP=tcm,
当t<5时,AQ=(10﹣2t)cm,
∴dP﹣AB=![]() ,dQ﹣AB=
,dQ﹣AB=![]() ,
,
∵dP﹣AB+dQ﹣AB=![]() ,∴
,∴![]() =
=![]() ,解得t=4;
,解得t=4;
当t≥5时,AQ=(2t﹣10)cm,
∴dP﹣AB=![]() ,dQ﹣AB=
,dQ﹣AB=![]() ,
,
∵dP﹣AB+dQ﹣AB=![]() ,∴
,∴![]() =
=![]() ,解得t=
,解得t=![]() ;
;
综上所述,t=4或![]() ;
;
拓展:设运动时间为t,
∵点P、Q同时到达点B,AB=12,AC+BC=20,
∴点P的速度:点Q速度=3:5,
设点P的速度为3x,点Q速度为5x,
∴dP﹣AB=n=![]() ,dQ﹣CB=
,dQ﹣CB=![]() ,
,
∴xt=4n,
∴dQ﹣CB=![]() =
=![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2x-2n=0有两个不相等的实数根,若n<5,且方程的两个实数根都是整数,则n的值为( )
A. n=2
B. n=0或n=1.5或n=4
C. n=4
D. n=0或n=1.5或n=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
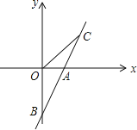
【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)
(1)求直线AB所对应的函数关系式;
(2)若直线AB上一点C在第一象限且点C的坐标为(a,2),求△BOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com