
 看图填空,并在括号内说明理由:
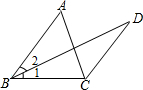
看图填空,并在括号内说明理由:分析 由BD为角平分线,利用角平分线定义得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与CD平行,利用两直线平行同旁内角互补即可求出所求角的度数.
解答 解:∵BD平分∠ABC(已知)
∴∠1=∠2(角平分线定义)
又∠1=∠D(已知)
∴∠2=∠D(等量代换)
∴AB∥CD(内错角相等两直线平行)
∴∠ABC+∠BCD=180°(两直线平行同旁内角互补)
又∠ABC=55°(已知)
∴∠BCD=125°.
故答案为:∠1;∠2;角平分线定义;∠2;∠D;等量代换;AB;CD;内错角相等两直线平行;∠BCD;两直线平行同旁内角互补;125°.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:选择题
| A. | m≤3 | B. | m≥3 | C. | m>3 | D. | m<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
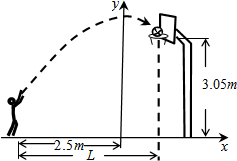 李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.
李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 8048个 | B. | 4024个 | C. | 4026个 | D. | 4028个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=(x-2)(x+3)+1 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com