
【题目】A、B两地之间有一C地,某日早上9点,一辆电力巡查车作例行巡查,查线路是从A地到C地再原路返回A地,全程匀速行驶,调头时间忽略不计.家住C地的陈先生同样是在当天的早上9点出发,驱车前往B地取一份文件,然后返回,经C地前往公司所在地A地.陈先生余程也是匀速行驶,取文件花费了4分钟,设两车之间的距离为ym,出发后的行驶时间为xmin,y与x的关系如图所示.那么当电力巡查车到达C地时,陈先生距A地还有_____m.

【答案】26000米.
【解析】
由图象过(0,12000)得到AC两地的路程,根据从C地到达B地的时间与距离得到巡查车的速度,进而得到两车速度的差,则可得陈先生开车速度为1000米/分;再根据C地到B地的路程得到巡查车到达C地的时间和陈先生返回的时间,进而得到答案.
解:图象过(0,12000),于是AC两地的路程为12000米,
由图象可知,经过25分钟,陈先生从C地到达B地,取文件的4分钟,两车距离减小了(29500﹣28300)=1200米,说明巡查车4分钟行驶1200米,因此巡查车的速度为300米/分,由图象可知两车速度的差为:(29500﹣12000)÷25=700米/分,因此陈先生开车速度为:1000米/分;从C地到B地的路程为25×1000=25000米;巡查车到达C地的时间为:12000÷300=40分,陈先生返回的时间为:40﹣29=11分,因此陈先生距A地的距离:(12000+25000)﹣11×1000=26000米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(1)求C点坐标,并判断b的正负性;
(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD与y轴交于点E,连接BC,
①若△BCE的面积为8,求二次函数的解析式;
②若△BCD为锐角三角形,请直接写出OA的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=﹣![]() (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=
(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=![]() (k>0,x>0)于点P,且OAMP=12,
(k>0,x>0)于点P,且OAMP=12,
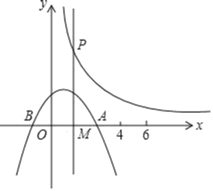
(1)求k值;
(2)当t=1时,求AB的长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x![]() ,且满足4x
,且满足4x![]() 6,通过L位置随t变化的过程,直接写出t的取值范围。
6,通过L位置随t变化的过程,直接写出t的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】休闲广场的边缘是一个坡度为i=1:2.5的缓坡CD,靠近广场边缘有一架秋千.秋千静止时,底端A到地面的距离AB=0.5m,B到缓坡底端C的距离BC=0.7m.若秋千的长OA=2m,则当秋千摆动到与静止位置成37°时,底端A′到坡面的竖直方向的距离A′E约为( )(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
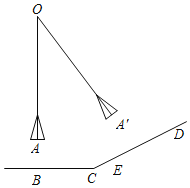
A. 0.4mB. 0.5mC. 0.6mD. 0.7m
查看答案和解析>>
科目:初中数学 来源: 题型:
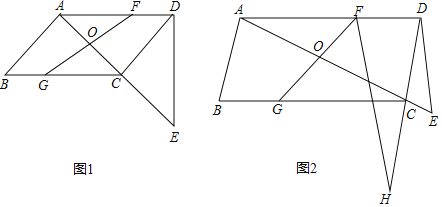
【题目】如图,在平行四边形ABCD中,AB⊥AC,过点D作DE⊥AD交直线AC于点E,点O是对角线AC的中点,点F是线段AD上一点,连接FO并延长交BC于点G.
(1)如图1,若AC=4,cos∠CAD=![]() ,求△ADE的面积;
,求△ADE的面积;
(2)如图2,点H为DC是延长线上一点,连接HF,若∠H=30°,DE=BG,求证:DH=CE+![]() FH.
FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
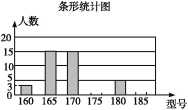
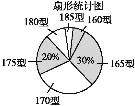
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
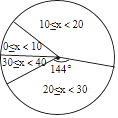
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
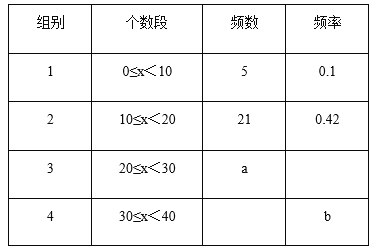
(1)表中的数a= ,b= ;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴交于两点,其中点A坐标(-1,0),点C(0,5)、D(1,8)在抛物线上,M为抛物线的顶点.
的图象与x轴交于两点,其中点A坐标(-1,0),点C(0,5)、D(1,8)在抛物线上,M为抛物线的顶点.
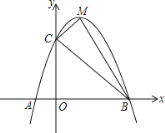
(1)求抛物线的解析式;
(2)求△MCB面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com