
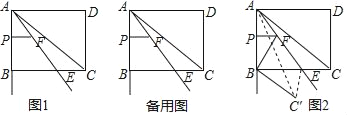
【题目】如图1,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE:CE=3:2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)线段AE= ;
(2)设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
(3)当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径;
(4)如图2,将△AEC沿直线AE翻折,得到△AEC',连结AC',如果∠ABF=∠CBC′,求t值.(直接写出答案,不要求解答过程).
【答案】(1)5;(2)y=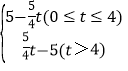 ;(3)12;(4)
;(3)12;(4)![]() .
.
【解析】(1)由矩形性质知BC=AD=5,根据BE:CE=3:2知BE=3,利用勾股定理可得AE=5;
(2)由PF∥BE知![]() ,据此求得AF=
,据此求得AF=![]() t,再分0≤t≤4和t>4两种情况分别求出EF即可得;
t,再分0≤t≤4和t>4两种情况分别求出EF即可得;
(3)由以点F为圆心的⊙F恰好与直线AB、BC相切时PF=PG,再分t=0或t=4、0<t<4、t>4这三种情况分别求解可得;
(4)连接CC′,交直线AE于点Q,先证△CQE∽△ABE得![]() ,据此求得CQ=
,据此求得CQ=![]() 、CC′=2CQ=
、CC′=2CQ=![]() ,再证△ABF∽△CBC′得
,再证△ABF∽△CBC′得![]() ,据此求得AF=
,据此求得AF=![]() ,根据
,根据![]() 可得答案.
可得答案.
(1)∵四边形ABCD为矩形,
∴BC=AD=5,
∵BE:CE=3:2,
则BE=3、CE=2,
∴AE=![]() =5,
=5,
故答案为:5;
(2)如图1,当点P在线段AB上运动时,即0≤t≤4,
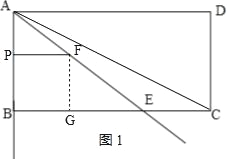
∵PF∥BE,
∴![]() ,即
,即![]() ,
,
∴AF=![]() ,
,
则EF=AE﹣AF=5﹣![]() ,即y=5﹣
,即y=5﹣![]() (0≤t≤4);
(0≤t≤4);
如图2,当点P在射线AB上运动时,即t>4,
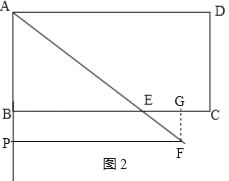
此时EF=AF﹣AE=![]() ﹣5,即y=
﹣5,即y=![]() ﹣5 (t>4);
﹣5 (t>4);
综上,y=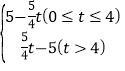 ;
;
(3)以点F为圆心的⊙F恰好与直线AB、BC相切时,PF=PG,
分以下三种情况:①当t=0或t=4时,显然符合条件的⊙F不存在;
②当0<t<4时,如图1,作FG⊥BC于点G,
则FG=BP=4﹣t,
∵PF∥BC,
∴△APF∽△ABE,
∴![]() ,即
,即![]() ,
,
∴PF=![]() t,
t,
由4﹣t=![]() t可得t=
t可得t=![]() ,
,
则此时⊙F的半径PF=![]() ;
;
③当t>4时,如图2,同理可得FG=t﹣4、PF=![]() t,
t,
由t﹣4=![]() t可得t=16,
t可得t=16,
则此时⊙F的半径PF=12;
(4)如图3,连接CC′,交直线AE于点Q,
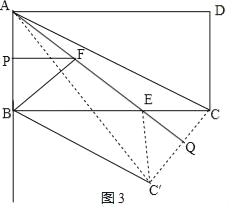
∵△CAQ≌△C′AQ,
∴AC=AC′、∠CAQ=∠C′AQ,
则∠CQE=∠ABE=90°,
∵∠CEQ=∠AEB,
∴△CQE∽△ABE,
∴![]() ,即
,即![]() ,
,
∴CQ=![]() ,
,
则CC′=2CQ=![]() ,
,
∵∠ABF=∠CBC′、∠BAE=∠ECC′,
∴△ABF∽△CBC′,
∴![]() ,即
,即![]() ,
,
解得: AF=![]() ,
,
由(2)知AF=![]() t,
t,
∴![]() ,
,
解得:t=![]() .
.


科目:初中数学 来源: 题型:
【题目】2018年11月2日﹣4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
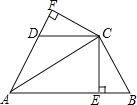
(1)BE与DF是否相等?请说明理由;
(2)若DF=1,AD=3,求AB的长;
(3)若△ABC的面积是23,△ADC面积是18,直接写出△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.
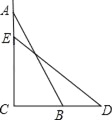
A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
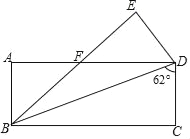
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两袋中各装有若干颗球,其种类与数量如表所示.今阿冯打算从甲袋中抽出一颗球,小潘打算从乙袋中抽出一颗球,若甲袋中每颗球被抽出的机会相等,且乙袋中每颗球被抽出的机会相等,则下列叙述何者正确?( )
甲袋 | 乙袋 | |
红球 | 2颗 | 4颗 |
黄球 | 2颗 | 2颗 |
绿球 | 1颗 | 4颗 |
总计 | 5颗 | 10颗 |
A. 阿冯抽出红球的机率比小潘抽出红球的机率大
B. 阿冯抽出红球的机率比小潘抽出红球的机率小
C. 阿冯抽出黄球的机率比小潘抽出黄球的机率大
D. 阿冯抽出黄球的机率比小潘抽出黄球的机率小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com