
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=![]() ,求BH的长.
,求BH的长.
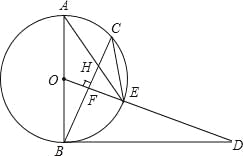
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,
∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,
即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;
(2)连接AC,如图1所示:
∵OF⊥BC,∴![]() , ∴∠CAE=∠ECB,
, ∴∠CAE=∠ECB,
∵∠CEA=∠HEC,∴△CEH∽△AEC,∴![]() ,∴CE2=EHEA;
,∴CE2=EHEA;
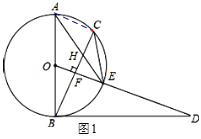
(3)连接BE,如图2所示:
∵AB是⊙O的直径,∴∠AEB=90°,
∵⊙O的半径为![]() ,sin∠BAE=
,sin∠BAE=![]() ,∴AB=5,BE=ABsin∠BAE=5×
,∴AB=5,BE=ABsin∠BAE=5×![]() =3,∴EA=
=3,∴EA=![]() =4,
=4,
∵![]() ,∴BE=CE=3,∵CE2=EHEA,∴EH=
,∴BE=CE=3,∵CE2=EHEA,∴EH=![]()
∴在Rt△ BEH中,BH=![]() =
=![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】设一列数![]() 、
、![]() 、
、![]() 、…、 a2010中任意三个相邻数之和都是35,已知a3=2x,a20=15,
、…、 a2010中任意三个相邻数之和都是35,已知a3=2x,a20=15, ![]() ,那么a2011=_________________。
,那么a2011=_________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
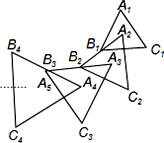
【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2,使A2B1=B1B2 ,以A2B2为边作等边△A2B2C2,A3为等边△A2B2C2的中心,连接A3B2并延长到点B3, 使A3B2=B2B3,以A3B3为边作等边△A3B3C3,依次作下去得到等边△AnBnCn,则等边△A6B6C6的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,E是BC上一点,且∠EAD =∠C,AD = 5,△ABE的周长是18,则梯形ABCD的周长为( )
A.23
B.26
C.28
D.29
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三阶幻方是由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的数表,要求其对角线、横行、纵向的和都相等。即为15,称这个幻方的幻和为15。四阶幻方是由1,2,3,……,15,16十六个数组成一个四行四列的数表,其对角线、横向、纵向的和都为同一个数,此数称为四阶幻方的幻和,那么此四阶幻方的幻和等于_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库某一天的原料进出记录如下表(运进用正数表示,运出用负数表示):
进出数量(吨) |
|
|
|
|
|
进出次数 |
|
|
|
|
|
(![]() )这天仓库的原料比原来增加了还是减少了?请说明理由.
)这天仓库的原料比原来增加了还是减少了?请说明理由.
(![]() )根据实际情况,现有两种方案.
)根据实际情况,现有两种方案.
方案一:运进每吨原料费用![]() 元,运出每吨原料费用
元,运出每吨原料费用![]() 元.
元.
方案二:不管运进还是运出费用都是每吨原料![]() 元.
元.
从节约运费的角度考虑,选用哪一种方案比较合适.
(![]() )在(
)在(![]() )的条件下,若该仓库某个月运进原料共
)的条件下,若该仓库某个月运进原料共![]() 吨,运出原料共
吨,运出原料共![]() 吨,当
吨,当![]() 、
、![]() 之间满足怎样的关系时两种方案吨运费相同.
之间满足怎样的关系时两种方案吨运费相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级一班在召开期末总结表彰会前,班主任安排班长李小波去商店买奖品,下面是李小波与售货员的对话:
李小波:阿姨,您好!
售货员:同学,你好,想买点什么?
李小波:我只有100元,请帮我安排买10支钢笔和15本笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com