
【题目】已知∠BAE与∠BCD互为补角,AB=AE,CB=CD,连接ED,点P为ED的中点.
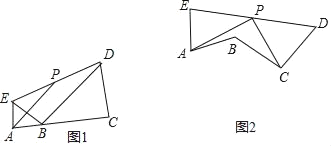
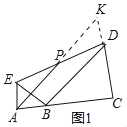
(1)如图1,若点A,B,C三点在同一条直线上.
①求证:∠EBD=90°;②求证:AP∥BD;
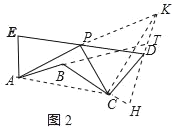
(2)如图2,若点A,B,C三点不在同一条直线上,求证:AP⊥CP.
【答案】(1)①见解析;②见解析;(2)见解析.
【解析】
(1)①设∠EAB=x,∠BCD=y,由∠BAE与∠BCD互为补角,得出x+y=180°,AE∥CD,由AE=AB,得出∠ABE=90°-![]() x,由CB=CD,得出∠CBD=90°-
x,由CB=CD,得出∠CBD=90°-![]() y,即可得出结论;
y,即可得出结论;
②延长AP交CD延长线于点K,由AE∥CD,得出∠EAP=∠DKP,由AAS证得△AEP≌△KDP,得出DK=AE=AB,证得CA=CK,得出∠CAP=90°-![]() y=∠CBD,即可得出结论;
y=∠CBD,即可得出结论;
(2)设∠EAB=x,∠BCD=y,延长AP到K,使PK=AP,连接KD,由SAS证得△AEP≌△KDP,得出KD=AE,∠EAP=∠DKP,AE∥KD,延长AB交KD于点T,延长KD交BC延长线于点H,则∠ATK=180°-∠EAB=180°-x=y,证得∠ATK=∠BCD=y,∠DCH=∠BTH,得出∠TBC=∠CDH,∠ABC=∠KDC,连接AC、KC,由SAS证得△ABC≌△KDC(SAS),得出CA=CK,即可得出结论.
(1)①设∠EAB=x,∠BCD=y,
∵∠BAE与∠BCD互为补角,
∴x+y=180°,AE∥CD,
∵AE=AB,
∴∠ABE=90°﹣![]() x,
x,
∵CB=CD,
∴∠CBD=90°﹣![]() y,
y,
∴∠EBD=180°﹣∠ABE﹣∠CBD=180°﹣90°+![]() x﹣90°+
x﹣90°+![]() y=
y=![]() (x+y)=90°;
(x+y)=90°;
②延长AP交CD延长线于点K,如图1所示:
∵AE∥CD,
∴∠EAP=∠DKP,
在△AEP和△KDP中, 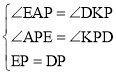
∴△AEP≌△KDP(AAS),
∴DK=AE=AB,
∵CB=CD,
∴CA=CK,
∴∠CAP=90°﹣![]() y=∠CBD,
y=∠CBD,
∴AP∥BD;
(2)设∠EAB=x,∠BCD=y,
∵∠BAE与∠BCD互为补角,
∴x+y=180°,
延长AP到K,使PK=AP,连接KD,如图2所示:
在△AEP和△KDP中,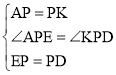
∴△AEP≌△KDP(SAS),
∴KD=AE,∠EAP=∠DKP,
∴AE∥KD,
延长AB交KD于点T,延长KD交BC延长线于点H,则∠ATK=180°﹣∠EAB=180°﹣x=y,
∴∠ATK=∠BCD=y,
∴∠DCH=∠BTH,
∵∠H=∠H,
∴∠TBC=∠CDH,
∴∠ABC=∠KDC,
连接AC、KC,
在△ABC和△KDC中, 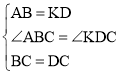
∴△ABC≌△KDC(SAS),
∴CA=CK,
∵PA=PK,
∴AP⊥CP.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政公司为绿化建设路风景带,计划购买甲乙两种树苗600株,甲种树苗每株50元,乙种树苗每株70元.有关统计表明,甲乙两种树苗的成活率分别为80%和95%.(注:成活率=![]() ×100%).
×100%).
(1)若购买树苗的钱不超过40000元,应如何选购甲、乙两种树苗;
(2)若希望这批树苗的成活率不低于90%,且购买树苗的费用最低,应如何选购甲、乙两种树苗并求出最低费用是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.
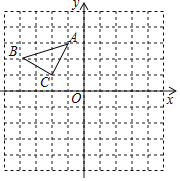
(1)画出把△ABC先向下平移3个单位,再向右平移4个单位后所得到的△A1B1C1;
(2)写出A1,B1,C1的坐标;
(3)求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).

(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com