
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
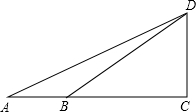 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
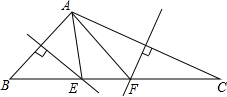 如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F.请找出图中相等的线段,并求△AEF的周长.
如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F.请找出图中相等的线段,并求△AEF的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
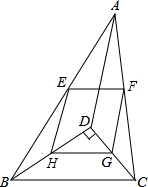 如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是线段AB,AC,CD,BD的中点.
如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是线段AB,AC,CD,BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com