
【题目】如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F.过点D作⊙O的切线交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
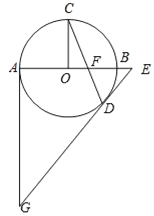
(1)求证:△EFD为等腰三角形;
(2)若OF:OB=1:3,⊙O的半径为3,求AG的长.
【答案】(1)见解析;(2)6
【解析】
(1)连接OD,只要证明∠EFD=∠EDF即可解决问题.
(2)先求得EF=1,设DE=EF=x,则OF=x+1,在Rt△ODE中,根据勾股定理求得DE=4,OE=5,根据切线的性质由AG为⊙O的切线得∠GAE=90°,再证明Rt△EOD∽Rt△EGA,根据相似三角形对应边成比例即可求得.
解:(1)证明:连接OD,
∵OC=OD,
∴∠C=∠ODC,
∵OC⊥AB,
∴∠COF=90°,
∴∠OCD+∠CFO=90°,
∵GE为⊙O的切线,
∴∠ODC+∠EDF=90°,
∵∠EFD=∠CFO,
∴∠EFD=∠EDF,
∴EF=ED.
(2)解:∵OF:OB=1:3,⊙O的半径为3,
∴OF=1,
∵∠EFD=∠EDF,
∴EF=ED,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=OE2,
∴32+x2=(x+1)2,解得x=4,
∴DE=4,OE=5,
∵AG为⊙O的切线,
∴AG⊥AE,
∴∠GAE=90°,
而∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AG=6.



 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在锐角三角形ABC中,AB=8,AC=5,BC=6,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,下列结论:①∠CBD=∠EBD,②DE⊥AB,③三角形ADE的周长是7,④![]() ,⑤
,⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
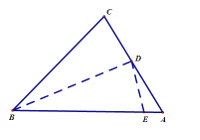
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
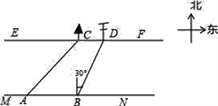
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度.(精确到0.1)(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.132)
≈1.132)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片OABC放在平面直角坐标系中,0为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠,使点A落在点Q处.
(1)如图①,当点Q恰好落在OB上时.求点p的坐标;
(2)如图②,当点P是AB中点时,直线OQ交BC于M点.
①求证:MB=MQ;②求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(m﹣1)x﹣m,其中m>0,它的图象与x轴从左到右交于R和Q两点,与y轴交于点P,点O是坐标原点.下列判断中不正确的是( )
A.方程x2﹣(m﹣1)x﹣m=0一定有两个不相等的实数根B.点R的坐标一定是(﹣1,0)
C.△POQ是等腰直角三角形D.该二次函数图象的对称轴在直线x=﹣1的左側
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办朗诵比赛,比赛结束后,对学生的成绩进行了统计.绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
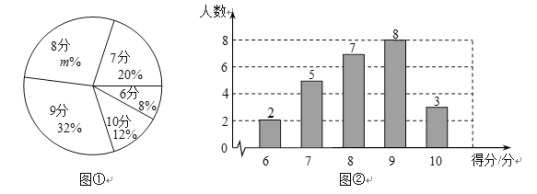
(1)参加这次比赛的人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组学生朗诵比赛成绩数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县政府计划拨款34000元为福利院购买彩电和冰箱,已知商场彩电标价为2000元/台,冰箱标价为1800元/台,如按标价购买两种家电,恰好将拨款全部用完.
(1)问原计划购买的彩电和冰箱各多少台?
(2)购买的时候恰逢商场正在进行促销活动,全场家电均降价![]() 进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com