

分析 (1)设一共调查了x名学生.因为课外阅读时间在0≤x<2的人数有10人,占10%,可得$\frac{10}{x}$×100%=10%,解方程即可.
(2)求出课外阅读时间在6≤x<8的人数有100-10-21-40-4=25人,即可画出图形.
(3)由课外阅读时间在4≤x<6的人数有40人,可得百分比,求出m的值,根据圆心角=360°×E组百分比,即可求出E组对应的圆心角度数.
(4)用样本估计总体的思想,即可解决问题.
解答 解:(1)设一共调查了x名学生.
∵课外阅读时间在0≤x<2的人数有10人,占10%,
∴$\frac{10}{x}$×100%=10%,
∴x=100,
∴一共调查了100名学生.
故答案为100.
(2)∵课外阅读时间在6≤x<8的人数有100-10-21-40-4=25人,可得补全后频数分布直方图如图所示,
(3)∵课外阅读时间在4≤x<6的人数有40人,
∴$\frac{40}{100}$×100%=40%,
∴m=40.
∵课外阅读时间在6≤x<8的人数有100-10-21-40-4=25,
∴E组对应的圆心角度数360°×4%=14.4°.
(4)∵100名学生中,课外阅读时间不小于6小时的学生有29人,占29%,
∴2000名学生,每周课外阅读时间不小于6小时的学生有估计有2000×29%=580人.
点评 本题考查频率分布直方图、扇形统计图、样本估计总体等知识,解题的关键是熟练掌握基本概念,灵活运用所学知识解决问题,属于中考常考题型.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,点F在AD上,$\frac{DF}{FA}$=$\frac{1}{2}$,BF与AC交于点P,BF与CD的延长线交于点G,连接DP并延长交AB于点E.
如图,在?ABCD中,点F在AD上,$\frac{DF}{FA}$=$\frac{1}{2}$,BF与AC交于点P,BF与CD的延长线交于点G,连接DP并延长交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
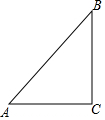 如图,在Rt△ABC中,∠C=90°,∠BAC=45°.
如图,在Rt△ABC中,∠C=90°,∠BAC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com