
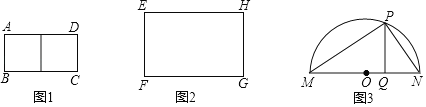
����Ŀ����1����ͼ1������ABCD���������߳�Ϊ1�������ι��ɣ������������ƴ��һ�������ABCD�����ȵ������Σ�
��2����ͼ2������EFGH�ij�FGΪ6����EFΪ4���ü��������Σ�Ȼ����ƴ�ӳ�һ�������EFGH�����ȵ������Σ������ü���ƴ�Ӻ��ͼ�Σ���Ҫ˵���ü��������ȷ���ģ������û���뵽�÷��������ü��������Ӧ�ԣ�ϸ��������ѧ��ʵ�����������а�����
��3����ͼ3���ڡ�O�У�MNΪֱ����PQ��MN������Ϊ��Q������O�ڵ�P������PM��PN����֤��PQ2��MQNQ���˽��ۿ�ֱ�����ã�
���𰸡���1������������2������������3��������
��������
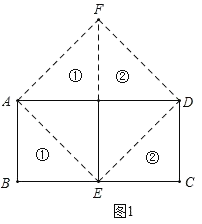
��1����ͼ1��ʾ���ֱ���AE��DE����һ��������ƴ����ԭ���������ȵ�������AEDF��
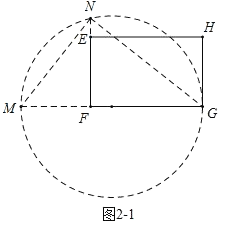
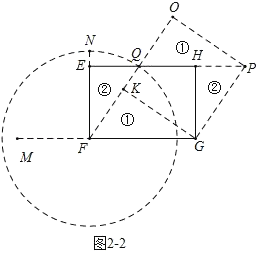
��2����ͼ2��1���ӳ�GF��M��ʹMF��EF��4������MGΪֱ����Բ���ӳ�FE��Բ�ڵ�N����![]() ��֪NF2��MFGF��EFGF��24����ͼ2��2����FΪԲ�ģ�FNΪ�뾶��Բ��������EH���ڵ�Q����G��GK��FQ�ڵ�K����FQ��GK�������ƴ��������KGPO����S������KGPO��24��
��֪NF2��MFGF��EFGF��24����ͼ2��2����FΪԲ�ģ�FNΪ�뾶��Բ��������EH���ڵ�Q����G��GK��FQ�ڵ�K����FQ��GK�������ƴ��������KGPO����S������KGPO��24��
��1����ͼ1��ʾ���ֱ���AE��DE����һ��������ƴ����ԭ���������ȵ�������AEDF��
��2����ͼ2��1���ӳ�GF��M��ʹMF��EF��4������MGΪֱ����Բ���ӳ�FE��Բ�ڵ�N��
���MNG=90��
���GNF+��MNF=90��,
�ߡ�NFM=90��,
���NMF+��MNF=90��,
���NMF=��GNF,
�֡�NFM=��NFG,
��![]()
��![]()
��NF2��MFGF��EFGF��24��
��S��������S������24��
��ͼ2��2����FΪԲ�ģ�FNΪ�뾶��Բ��������EH���ڵ�Q����G��GK��FQ�ڵ�K��
��FQ��GK�������ƴ��������KGPO����S������KGPO��24��


 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д� С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A����5��0����B����3��0����C��y���������ϣ���CBO��45�㣬CD��AB����CDA��90�㣬��P�ӵ�A��������x��������ÿ��1����λ���ȵ��ٶ��˶����˶�ʱ��Ϊt�룮
��1����ʱt��1����PC�ij���
��2������BCP��15��ʱ����t��ֵ��
��3�����߶�PCΪֱ���ġ�Q���P���˶����仯������Q���ı���ABCD�ıߣ�������ڵ�ֱ�ߣ�����ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ���ڡ�����Σ�շ����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ�˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������ˣ�
��1������ѡȡ�����ķ����������һ���� ����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����γ������˷��֣����ܵ��˵ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��
��m= ��n= ��
����ȫ����ͳ��ͼ��
������ͳ��ͼ������C��Բ�ĽǶ����� ��
����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
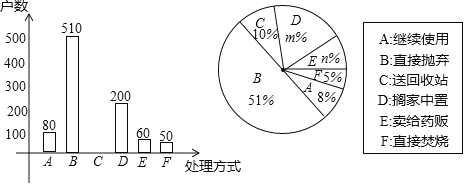
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ij������Ʒר��������7�������9�������������Ϊ355Ԫ������10�������20�������������Ϊ650Ԫ��
��1����ÿ�������ÿ���������������
��2����֪ÿ������Ľ���Ϊ200Ԫ��ÿ������Ľ���Ϊ160Ԫ������ר����ƻ��ò�����17400Ԫ�������������100������Ҫ��������������������������һ�룬����Ϊר������Ʒ���Ҫ��Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ����Ժ���ز�����������ʹ����������������ij�мӿ������ⷿ�Ľ���������2011����������Ͷ��2��Ԫ����ҽ��������ⷿ8��ƽ������Ԥ�Ƶ�2013������깲�ۼ�Ͷ��9.5��Ԫ����ҽ������ⷿ��������������ÿ��Ͷ�ʵ���������ͬ��
(1)��ÿ��������Ͷ�ʵ������ʣ�
(2)���������ڵĽ���ɱ���������2013��������˶�����ƽ�������ⷿ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ACΪ��O��ֱ����MNΪ��O�����ߣ���DΪ�е㣬����AD��ֱ��MN��ֱ��AC���ڵ�B������A��AE��MN������ΪE��
��1����֤��ADƽ�֡�EAB��
��2����֤��AD2��AGAB��
��3����AE��6![]() ��BE��8
��BE��8![]() ����BC�ij���
����BC�ij���
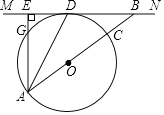
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x+m��2=0������ʵ������mΪ���������Ҹ÷��̵ĸ��������������������������������m�ĺ�Ϊ��������
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90����D��BC����һ�㣬��BAD��45����AC��3��AB��![]() ����BD�ij���
����BD�ij���
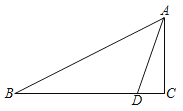
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��x��![]() �������߾�����A��6��0����B��0��4����
�������߾�����A��6��0����B��0��4����
��1���������߽���ʽ���������ꣻ
��2�����E��x��y������������һ���㣬��λ�ڵ������ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ����ı���OEAF�����S��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3�������ı���OEAF�����Ϊ24ʱ�����ж�OEAF�Ƿ�Ϊ���Σ�
���Ƿ���ڵ�E��ʹ�ı���OEAFΪ�����Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
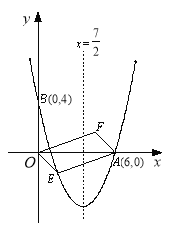
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com