
【题目】已知二次函数![]() 同时满足下列条件:对称轴是
同时满足下列条件:对称轴是![]() ;最值是
;最值是![]() ;二次函数的图象与
;二次函数的图象与![]() 轴有两个交点,其横坐标的平方和为
轴有两个交点,其横坐标的平方和为![]() ,则
,则![]() 的值是( )
的值是( )
A. ![]() 或
或![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
【答案】C
【解析】
由在x=1时取得最大值15,可设解析式为:y=a(x-1)2+15,只需求出a即可,又与x轴交点横坐标的平方和为15-a,可求出a,所以可求出解析式得到b的值.
解:解法一:∵x轴上点的纵坐标是0,
∴由题可设抛物线与x轴的交点为( 1-t,0),( 1+t,0),其中t>0,
∵两个交点的横坐标的平方和等于15-a即:(1-t)2+(1+t)2=15-a,
可得t=![]() ,
,
由顶点为(1,15),
可设解析式为:y=a(x-1)2+15,
将(1-![]() ,0)代入解析式,
,0)代入解析式,
得a=-2或a=15(不合题意,舍去)
∴y=-2(x-1)2+15=-2x2+4x+13,
∴b=4;
解法二:∵对称轴是x=1,最值是15,
∴设y=ax2+bx+c=a(x-1)2+15,
∴y=ax2-2ax+15+a,
设方程ax2-2ax+15+a=0的两个根是x1,x2,
则x1+x2=![]() =2,x1x2=
=2,x1x2=![]() ,
,
∵二次函数的图象与x轴有两个交点,其横坐标的平方和为15-a,
(x1)2+(x2)2=(x1+x2)2-2x1x2=15-a,
∴![]() =15-a,
=15-a,
a2-13a-30=0,
a1=15(不合题意,舍去),a2=-2,
∴y=-2(x-1)2+15=-2x2+4x+13;
∴b=4.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市为支援灾区建设,计划向![]() 、
、![]() 两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到
两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到![]() 、
、![]() 两地的每吨物资的运费如表所示:
两地的每吨物资的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设甲地运到![]() 地的急需物资为
地的急需物资为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并写出
(吨)的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求最低总运费,并说明总运费最低时的运送方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
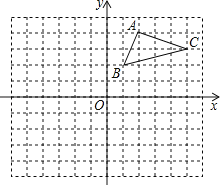
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标( , );
(2)将△ABC的三个顶点的横、纵坐标都乘以﹣1,分别得到对应点A2,B2,C2,请画出△A2B2C2,并说明△A1B1C1和△A2B2C2是否是轴对称图形,如果是,那么它们的对称轴是什么?如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
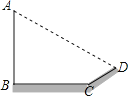
【题目】如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:![]() ,且此时测得1米杆的影长为2米,则电线杆的高度为( )
,且此时测得1米杆的影长为2米,则电线杆的高度为( )
A.(14+2![]() )米 B.28米 C.(7+
)米 B.28米 C.(7+![]() )米 D.9米
)米 D.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点D为直线
,点D为直线![]() 上的个动点(不与B、C重合),连结
上的个动点(不与B、C重合),连结![]() ,将线段
,将线段![]() 绕点D按顺时针方向旋转90°,使点A旋转到点E,连结
绕点D按顺时针方向旋转90°,使点A旋转到点E,连结![]() .
.
(问题初探)如果点D在线段![]() 上运动,通过观察、交流,小明形成了以下的解题思路:过点E作
上运动,通过观察、交流,小明形成了以下的解题思路:过点E作![]() 交直线
交直线![]() 于F,如图2所示,通过证明
于F,如图2所示,通过证明![]() ______,可推证
______,可推证![]() 是_____三角形,从而求得
是_____三角形,从而求得![]() ______°.
______°.
(继续探究)如果点D在线段![]() 的延长线上运动,如图3所示,求出
的延长线上运动,如图3所示,求出![]() 的度数.
的度数.
(拓展延伸)连接![]() ,当点D在直线
,当点D在直线![]() 上运动时,若
上运动时,若![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
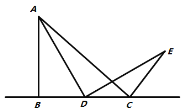
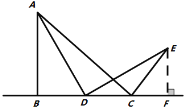
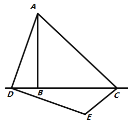
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红爸爸从家骑电瓶车出发,沿一条直路到相距2400m的学校接小红回家,小红爸爸出发的同时,小红以96m/min的速度从学校沿同一条道路步行回家,小红爸爸赶到学校校门口等候2min后知道小红已离校,立即沿原路以原速返回,设他们出发的时间为t min,图示中的折线OABD表示小红爸爸与家之间的距离S1与t之间的函数关系,线段EF表示小红与家之间的距离S2与t之间的函数关系,则小红爸爸从家出发在返回途中追上小红的时间是( )
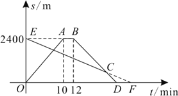
A.12minB.16minC.18minD.20min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距![]() km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(-x)=-sinx,cos(-x)=cosx,sin(x+y)=sinx·cosy+cosx·siny.据此判断下列等式成立的是_________(填序号).
①cos(-60°)=—cos60°=![]()
②sin75°=sin(30°+45°)=sin30°·cos45°+cos30°·sin45°=![]()
③sin2x=sin(x+x)=sinx·cosx+cosx·sinx=2sinx·cosx;
④sin(x-y)=sinx·cosy-cosx·siny.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市区九年级学生每天的健身活动情况,随机从市区九年级的12000名学生中抽取了500名学生,对这些学生每天的健身活动时间进行统计整理,作出了如下不完整的统计图(每组数据含最小值不含最大值,统计数据全部为整数),请根据以下信息解答如下问题:
时间/分 | 频数 | 频率 |
30~40 | 25 | 0.05 |
40~50 | 50 | 0.10 |
50~60 | 75 | b |
60~70 | a | 0.40 |
70~80 | 150 | 0.30 |
(1)a=_______,b=_______;
(2)请补全频数分布直方图;
(3)学生每天健身时间的中位数会落在哪个时间段?
(4)若每天健身时间在60分钟以上为符合每天“阳光一小时”的规定,则符合规定的学生人数大约是多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com