
【题目】已知:如图,在△ABC中,∠ABC=45°,![]() ,AB=14,
,AB=14,
(1)求:△ABC的面积;
(2)若以C为圆心的圆C与直线AB相切,以A为圆心的圆A与圆C相切,试求圆A的半径.
【答案】(1)42;(2) 4或16
【解析】
(1)过C作CD⊥AB于D解直角三角形得到CD,根据三角形的面积公式即可得到结论;(2)根据圆C与直线AB相切,得到○C的半径,根据勾股定理得到AC,设○A的半径为r,当圆A与圆C内切时,当圆A与圆C外切时即可得到结论
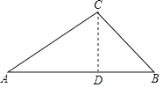
(1)过C作CD⊥AB于D,
∵![]() ,
,
∴![]() ,
,
∵∠ABC=45°,
∴BD=CD,
∵AB=14,
∴![]() ,
,
∴CD=6,
∴△ABC的面积![]() ;
;
(2)∵以C为圆心的圆C与直线AB相切,
∴⊙C的半径=6,
∵AD=8,
∴![]() ,
,
设⊙A的半径为r,
当圆A与圆C内切时,r﹣6=10,
∴r=16,
当圆A与圆C外切时,r+6=10,
∴r=4,
综上所述:以A为圆心的圆A与圆C相切,圆A的半径为:4或16.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4.
(1)求抛物线的表达式;
(2)求∠CAB的正切值;
(3)如果点P是x轴上的一点,且∠ABP=∠CAO,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 的边
的边![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,边AC绕着点A逆时针旋转
,边AC绕着点A逆时针旋转![]() 得到
得到![]() ,联结
,联结![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“双旋三角形”.如果等边
的“双旋三角形”.如果等边![]() 的边长为a,那么它的“双旋三角形”的面积是__________(用含a的代数式表示).
的边长为a,那么它的“双旋三角形”的面积是__________(用含a的代数式表示).
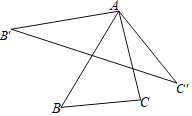
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
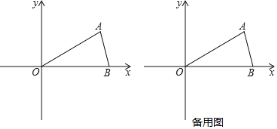
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
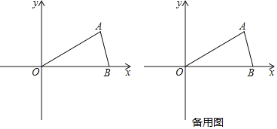
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
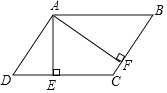
【题目】如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设![]() ,如果向量
,如果向量![]() ,那么k的值是_____.
,那么k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
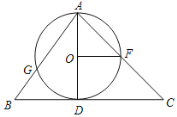
【题目】已知△ABC中,AD⊥BC,垂足为D,且AD=4,以AD为直径作圆O,交AB边于点G,交AC边于点F,如果点F恰好是![]() 的中点.
的中点.
(1)求CD的长度.
(2)当BD=3时,求BG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法
①一共测试了36名男生的成绩.
②立定跳远成绩的中位数分布在1.8~2.0组.
③立定跳远成绩的平均数不超过2.2.
④如果立定跳远成绩1.85米以下(不含1.85)为不合格,那么不合格人数为6人.
正确的是( )
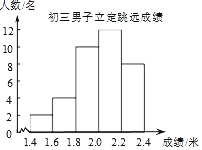
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
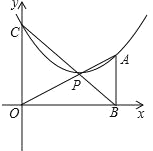
【题目】如图,A(2,1),B(2,0),C为y轴上一动点,过A,C两点的抛物线为:y=ax2+bx+n(a≠0,a≠﹣1),直线OA与直线BC交于点P,
(1)若n=1,且抛物线恰好也过P点,直接写出抛物线顶点坐标为:(_____,______)
(2)当抛物线同时经过A,C,P三点时,此时P必为该抛物线的顶点,请以n=2为例验证上述结论的正确性.
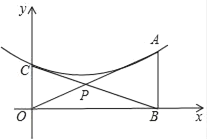
(3)若抛物线与直线BC有唯一交点C,
①求a的值;并求当C沿y轴向上运动时,其顶点同时向下运动所对应n的取值范围;
②设过B另有一直线(与BC、AB不重合),也与抛物线仅有一个交点,设为D,经探究发现:无论C在y轴上如何运动,直线CD一定经过一个确定不动点Q.请直接写出该不动点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com