
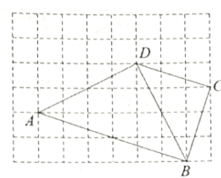
【题目】利用6×8正方形网格画图(不写画法,保留画图痕迹):
(1)画出![]() 的对称轴直线
的对称轴直线![]() ;
;
(2)画![]() ,使得
,使得![]() 与
与![]() 关于直线
关于直线![]() 对称;
对称;
(3)画格点![]() ,使得
,使得![]() 是以
是以![]() 为斜边的直角三角形。
为斜边的直角三角形。
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先判断出△ABD为等腰直角三角形,再判断出格点M为AB中点,则过点D、M作直线即为对称轴l;
(2)先判断出CD⊥l,然后延长CD至E,使CD=DE,最后连接即可;
(3)根据∠AFB是直角且点F在格点上进行判断即可.
解:(1)由勾股定理得,![]() ,
,
∴△ABD为等腰直角三角形,
由勾股定理得,AM=![]() ,BM=
,BM=![]() ,AB=
,AB=![]() ,
,
∴AM=BM=![]() AB,即点M 为AB中点,
AB,即点M 为AB中点,
∴过点D、M作直线l即为△ABD的对称轴;
(2)∵△ABD为等腰直角三角形,直线l⊥AB,
∴直线l与BD相交所成锐角为45°,
∵由勾股定理得,![]() ,
,
∴△BCD为等腰直角三角形,则∠BDC=45°,
∴CD⊥l,
如图,延长CD至E,使CD=DE,连接AE,则△ADE即为所求;
(3)如图,在△ABF1中,AF12=4,BF12=36,AB2=22+62=40,
∴AF12+BF12=AB2,
∴△ABF1是直角三角形,∠AF1B=90°,则点F1即为所求,
同理可得,点F2、F3、F4即为所求.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的顶点
的顶点![]() 为坐标原点,顶点
为坐标原点,顶点![]() 在
在![]() 轴正半轴上,顶点
轴正半轴上,顶点![]() 、
、![]() 在第一象限,
在第一象限,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,将四边形
上,将四边形![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 和点
和点![]() 分别落在这个坐标平面内的
分别落在这个坐标平面内的![]() 和
和![]() 处,且
处,且![]() ,某正比例函数图象经过
,某正比例函数图象经过![]() ,则这个正比例函数的解析式为( )
,则这个正比例函数的解析式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=10,AB=14,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点![]() 落在∠ABC的角平分线上时,DE的长为_______.
落在∠ABC的角平分线上时,DE的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象的顶点坐标为(3,-2),且与y轴交于(0,![]() ).
).
(1)求函数的解析式;
(2)若点(p,m)和点(q,n)都在该抛物线上,若p>q>5,判断m和n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某列车平均提速80km/h,用相同的时间,该列车提速前行驶300km,提速后比提速前多行驶200km,求该列车提速前的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com