
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
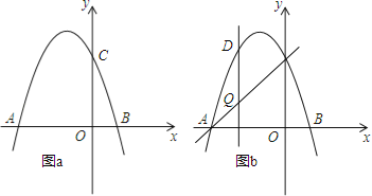
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
【答案】(1)y=﹣x2﹣2x+3(2)(﹣1,4)或(﹣1+![]() ,﹣4)或(﹣1﹣
,﹣4)或(﹣1﹣![]() ,﹣4);(3)
,﹣4);(3)![]() .
.
【解析】
试题分析:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,然后解方程组即可;(2)先求出点B的坐标(1,0),然后利用S△AOP=4S△BOC,求出点P的横坐标,代入y=﹣x2﹣2x+3即可求出纵坐标;(3)用待定系数法求成直线AC的解析式y=x+3,设出Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),然后用x表示出线段DQ长度,利用配方法可确定其最大值.
试题解析:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得![]() .
.
解得![]() .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3
(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4×![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±![]() .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+![]() ,﹣4)或(﹣1﹣
,﹣4)或(﹣1﹣![]() ,﹣4);
,﹣4);
(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得![]() ,
,
解得![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
【题目】从我市至枣庄正在修筑的高速公路经过某村,需把本村部分农户搬迁至一个规划区域建房.若这批搬迁农户建房每户占地![]() ,则规划区域内绿地面积占规划区域总面积的
,则规划区域内绿地面积占规划区域总面积的![]() ;政府又鼓励本村不需要搬迁的农户到规划区域建房,这样又有
;政府又鼓励本村不需要搬迁的农户到规划区域建房,这样又有![]() 户农户加入建房,若仍以每户占地
户农户加入建房,若仍以每户占地![]() 计算,则这时绿地面积只占规划区域总面积的
计算,则这时绿地面积只占规划区域总面积的![]() .问:
.问:
(1)(列方程组解应用题)最初必须搬迁建房的农户有多少,政府的规划区域总面积是多少平方米?
(2)若要求绿地面积不得少于规划区域总面积的![]() ,为了符合要求,需要退出部分农户,至少需要退出几户农户?
,为了符合要求,需要退出部分农户,至少需要退出几户农户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题2019年是决胜全面建成小康社会、打好污染防治攻坚战的关键之年.为了解决垃圾回收最后一公里的难题,“小黄狗”智能垃圾分类回收环保公益项目通过大数据、人工智能和物联网等先进科技进驻小区、写字楼、学校、机关和社区等进行回收.某位小区居民装修房屋,在过去的一个月内投放纸类垃圾和塑料垃圾共82公斤,其中纸类垃圾的投放是塑料垃圾的8倍多10公斤,请问这位小区居民在过去的一个月内投放纸类垃圾和塑料垃圾分别是多少公斤?

查看答案和解析>>
科目:初中数学 来源: 题型:
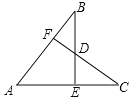
【题目】如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
A. ![]() B.
B. ![]() C. 点D在
C. 点D在![]() 的平分线上D. 点D是CF的中点
的平分线上D. 点D是CF的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
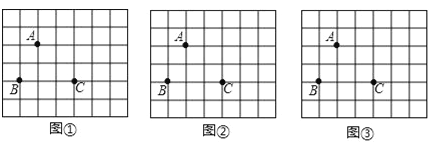
【题目】如图,均为7×6的正方形网格,点A、B、C均在格点(小正方形的顶点)上,在图中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其满足下列条件(三个图形互不相同):
(1)在图①中所画的四边形中,∠D为钝角,且四边形是轴对称图形.
(2)在图②中所画的四边形中,∠D为锐角,且四边形是中心对称图形.
(3)在图③所画的四边形中,∠D为直角,且四边形面积为5平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移得到△A1B1C1的面积.求:
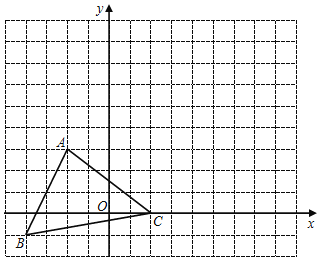
(1)画出△A1B1C1和写出点B1的坐标;
(2)写出平移的过程;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为常数),下列说法正确的是( ).
为常数),下列说法正确的是( ).
A. 对任意实数![]() ,函数与
,函数与![]() 轴都没有交点
轴都没有交点
B. 存在实数![]() ,满足当
,满足当![]() 时,函数
时,函数![]() 的值都随
的值都随![]() 的增大而减小
的增大而减小
C. ![]() 取不同的值时,二次函数
取不同的值时,二次函数![]() 的顶点始终在同一条直线上
的顶点始终在同一条直线上
D. 对任意实数![]() ,抛物线
,抛物线![]() 都必定经过唯一定点
都必定经过唯一定点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com