练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知函数y=（x-2）（x-4），当m≤x≤m+1时，求y的最小值．

    分析 先求出抛物线对称轴x=3，然后分m≤3，m＞3两种情况，根据二次函数的增减性解答．

    解答 解：函数y=（x-2）（x-4）的对称轴是x=3，
    ∴当x≤3时，y随x的增大而减小，
    ∴m＜2，此时x=m+1时取最小值m2-4m+3；2≤m≤3时，最小值是-1；m＞3时，x=m取最小值m2-6m+8．

    点评 本题考查了二次函数的最值问题，主要利用了二次函数的增减性，注意根据二次函数的对称轴分情况讨论求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

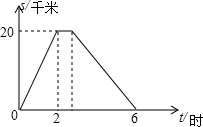    17．在一条笔直的公路上，依次有A、C、B三地．小明从A地途经C地前往距A地20千米的B地，到B地休息一段时间后立即按原路返回到A地．小明出发4小时的时候距离A地12千米．小明去时从C地到B地，返回时再由B地到C地（包括在B地休息的时间）共用2小时．他与A地的距离s（单位：千米）和所用的时间t（单位：小时）之间的函数关系如图所示．下列说法：①小明去时的速度为10千米/时；②小明在B地休息了$\frac{2}{3}$小时；③小明回来时的速度为6千米/时；④C地与A地的距离为15千米，其中正确的个数为（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，正方形ABCD是一块绿化带，其中阴影部分EFGH是正方形花圃．一只小鸟随机落在绿化带区域内，则它停留在花圃上的概率是$\frac{2}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图1，已知△ABC中，AB=AC，现在△ABC外作∠ACP=∠ACB，在BC上取一点D，在CP上取一点E，使BD=CE，并连接AD，AE．
    （1）求证：AD=AE；
    （2）若∠BCP=144°，求∠DAE的度数；
    （3）如图2，若AD⊥BC，过点E作EF∥BC交AC于点F，连接DF．试判断四边形CDFE的形状，并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

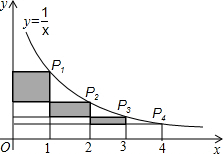    2．在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，有点P1，P2，…，P2011，…，它们的横坐标依次为1，2，…2011，…分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1，S2，…，S2010…，则S1+S2+…+S2010=$\frac{2010}{2011}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

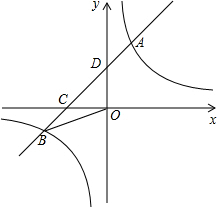    12．如图，在平面直角坐标系中，一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于一、三象限的A、B两点，与x轴交于点C，与y轴交于点D，已知点B的坐标为（-5，-2），C为BD的中点．
    （1）求出k的值；
    （2）求一次函数的解析式；
    （3）利用函数图象求关于x的不等式ax+b＜$\frac{k}{x}$的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．用科学计算器计算：$\root{3}{48}$sin48°≈2.70．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．已知5个正数a1，a2，a3，a4，a5的平均数是a，且a1＞a2＞a3＞a4＞a5，则数据a1，a2，a3，0，a4，a5的平均数和中位数是（　　）
    A．a，$\frac{{a}_{3}}{2}$B．a，$\frac{{a}_{3}+{a}_{4}}{2}$C．$\frac{5}{6}$a，$\frac{{a}_{3}+{a}_{4}}{2}$D．$\frac{5}{6}$a，$\frac{{a}_{3}}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．“五一”节老同学聚会，每两个人都握一次手，所有人共握手28次，则参加聚会的人数是（　　）
    A．7B．8C．9D．10

    查看答案和解析>>

    同步练习册答案