
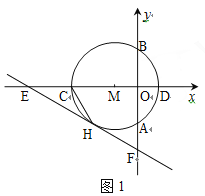
【题目】如图1,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=-![]() x-
x-![]() 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.
(1)请直接写出OE、⊙M的半径r、CH的长;
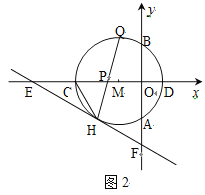
(2)如图2,弦HQ交x轴于点P,且DP : PH=3 : 2,求cos∠QHC的值;
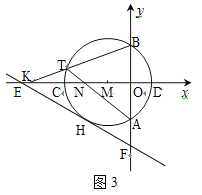
(3)如图3,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
【答案】(1)OE=5,r=2,CH=2
(2)![]() ;
;
(3)a=4
【解析】
(1)在直线y=-![]() x-
x-![]() 中,令y=0,可求得E的坐标,即可得到OE的长为5;连接MH,根据△EMH与△EFO相似即可求得半径为2;再由EC=MC=2,∠EHM=90°,可知CH是RT△EHM斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长;
中,令y=0,可求得E的坐标,即可得到OE的长为5;连接MH,根据△EMH与△EFO相似即可求得半径为2;再由EC=MC=2,∠EHM=90°,可知CH是RT△EHM斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长;
(2)连接DQ、CQ.根据相似三角形的判定得到△CHP∽△QPD,从而求得DQ的长,在直角三角形CDQ中,即可求得∠D的余弦值,即为cos∠QHC的值;
(3)连接AK,AM,延长AM,与圆交于点G,连接TG,由圆周角定理可知,
∠GTA=90°,∠3=∠4,故∠AKC=∠MAN,再由△AMK∽△NMA即可得出结论.
(1)OE=5,r=2,CH=2
(2)如图1,连接QC、QD,则∠CQD =90°,∠QHC =∠QDC,
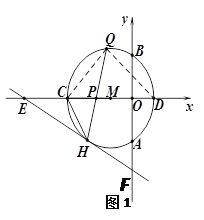
易知△CHP∽△DQP,故![]() ,得DQ=3,由于CD=4,
,得DQ=3,由于CD=4,
![]() ;
;
(3)如图2,连接AK,AM,延长AM,
与圆交于点G,连接TG,则![]()

![]()
![]() ,
,![]()
由于![]() ,故,
,故,![]() ;
;
而![]() ,故
,故![]()
在![]() 和
和![]() 中,
中,![]() ;
;![]()
故△AMK∽△NMA
![]() ;
;![]()
即:![]()
故存在常数![]() ,始终满足
,始终满足![]()
常数a="4"
解法二:连结BM,证明![]() ∽
∽![]()
得![]()


科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2(k3)x3在x=0和x=4时的函数值相等.
(1)求该二次函数的表达式;
(2)画出该函数的图象,并结合图象直接写出当y<0时,自变量x的取值范围;
(3)已知关于x的一元二次方程![]() ,当1≤m≤3时,判断此方程根的情况.
,当1≤m≤3时,判断此方程根的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
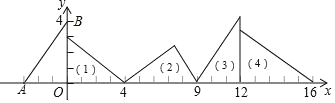
【题目】如图,在直角坐标系中,已知点 A(﹣3,0),B(0,4),对△OAB 连续作旋转变换,依次得到三角形(1),(2),(3),(4)…,则三角形(2019)的直角顶点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
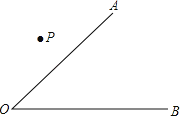
【题目】如图,已知∠AOB和点P.
(1)过点P画射线PM∥OA,PN∥OB,符合要求的图形有哪几种情况?请分别画出这些图形;
(2)在所画的图形中,∠MPN与∠AOB的大小有什么关系?
(3)你有什么发现?
查看答案和解析>>
科目:初中数学 来源: 题型:
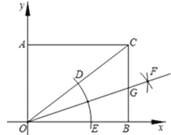
【题目】如图,已知矩形 AOBC 的三个顶点的坐标分别为 O(0,0),A(0,3), B(4,0),按以下步骤作图:①以点 O 为圆心,适当长度为半径作弧, 分别交 OC,OB 于点 D,E;②分别以点 D,E 为圆心,大于 ![]() DE 的长为半径作弧,两弧在∠BOC 内交于点 F;③作射线 OF,交边 BC于点 G,则点 G 的坐标为( )
DE 的长为半径作弧,两弧在∠BOC 内交于点 F;③作射线 OF,交边 BC于点 G,则点 G 的坐标为( )
A. (4, ![]() )B. (
)B. ( ![]() ,4)C. (
,4)C. ( ![]() ,4)D. (4,
,4)D. (4, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com