
(本题14分)如图,抛物线 与
与 轴相交于
轴相交于 、
、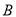 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.


(1)求出 、
、 两点的坐标和抛物线的对称轴;
两点的坐标和抛物线的对称轴;
(2)连接 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点 ,点
,点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 交抛物线于点
交抛物线于点 ,设点
,设点 的横坐标为
的横坐标为 ;
;
①用含 的代数式表示线段
的代数式表示线段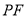 的长,并求出当
的长,并求出当 为何值时,四边形
为何值时,四边形 为平行四边形?
为平行四边形?
②设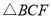 的面积为
的面积为 ,求
,求 与
与 的函数关系式.
的函数关系式.
(3)若点G为抛物线上的一个动点,在x轴上是否存在这样的点H,使以B、C、G、H为顶点的四边形是平行四边形?如果存在,直接写出满足条件的H点的坐标;如果不存在,请说明理由.
(1)B(3,0),C(0,3),抛物线的对称轴是x=1;
(2)①当m=2时,四边形PEDF为平行四边形;②S= (0≤m≤3).
(0≤m≤3).
(3)H坐标为H1(1,0)或H2(5,0)或H3( ,0)m的变化范围是0≤m≤3
,0)m的变化范围是0≤m≤3
【解析】
试题分析:(1)令y=0,则﹣x2+2x+3=﹣(x+1)(x﹣3)=0,
解得,x=﹣1或x=3,则A(﹣1,0),B(3,0).
所以,对称轴是x= =1.
=1.
令x=0,则y=0,则C(0,3).
综上所述, B(3,0),C(0,3),抛物线的对称轴是x=1;
(2)①设直线BC的函数关系式为:y=kx+b(k≠0).
把B(3,0),C(0,3)分别代入得: ,
,
解得:k=﹣1,b=3.
所以直线BC的函数关系式为:y=﹣x+3.
当x=1时,y=﹣1+3=2,
∴E(1,2).
当x=m时,y=﹣m+3,
∴P(m,﹣m+3).
在y=﹣x2+2x+3中,当x=1时,y=4.
∴D(1,4)
当x=m时,y=﹣m2+2m+3,
∴F(m,﹣m2+2m+3)
∴线段DE=4﹣2=2,
线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m
∵PF∥DE,
∴当PF=ED时,四边形PEDF为平行四边形.
由﹣m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得:OB=OM+MB=3.
 =
= .
.
m的变化范围是0≤m≤3.
(3)若以B、C、G、H为顶点的四边形是平行四边形,
①BH为四边形的边,则CG//BH
故点G和点C关于直线x=1对称
∴G(2,3)且CG=2
此时BH=2
∴H1(1,0)或H2(5,0)
②BH为对角线,则此时G的纵坐标为-3
∴﹣x2+2x+3=-3,可得x= .有图象可知x=
.有图象可知x= 舍去
舍去
故G(3,  )
)
B、H关于点( ,0)
,0)
所以H( ,0)
,0)
综上,H坐标为H1(1,0)或H2(5,0)或H3( ,0)
,0)
考点:抛物线的综合运用


科目:初中数学 来源: 题型:
| k |
| x |
A、2
| ||
B、±2
| ||
C、
| ||
D、±
|
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市联盟学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. B.8 C.
B.8 C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知A,B,C是⊙O上不同的三个点,∠AOB=60°,则∠ACB=( )
A.60° B.30° C.60°或120° D.30°或150°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级上学期第二次月考数学试卷(解析版) 题型:选择题
如图,函数 的图象与x轴的一个交点坐标为(3,0),则另一交点的横坐标为( )
的图象与x轴的一个交点坐标为(3,0),则另一交点的横坐标为( )

A.-4 B.-3 C.-2 D.-1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题8分)在梯形ABCD中,AD//BC,连结AC,且AC=BC,在对角线AC上取点E,使CE=AD,连接BE.

(1)求证:△DAC≌△ECB;
(2)若CA平分∠BCD,且AD=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市萧山区高桥教育九年级上学期第二次检测数学试卷(解析版) 题型:解答题
(本小题满分10分)某经销店为某工厂代销一种建筑材料.当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校八年级上学期期中数学试卷(解析版) 题型:填空题
已知△ABC中,∠A:∠B:∠C=1:1:2,则这个三角形是 三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com