
����Ŀ����ͼ���ش���������
��֪����ͼ��ÿһС��λ����Ϊ1cm��������ABCD�Ķ��㶼�ڷ���Ķ����ϣ���������ABCD�Ƶ�A��ʱ����ת90���õ��ı���AB1C1D1.
��1�������ı���AB1C1D1
��2��������ı���AB1C1D1������AB��������ƽ��x cm��
�ٵ��߶�C1D1���߶�AD�����ʱ���ú�x�Ĵ���ʽ��ʾ�ı���AB1C1D1�볤����ABCD�ص����ֵ����S.
�����ı���AB1C1D1�볤����ABCD�ص����ֵ����Ϊ4.5 cm2ʱ����x��ֵ.

���𰸡���1�������
��2����![]()
�ڵ�![]() ��6.5ʱ���ı���AB1C1D1�볤����ABCD�ص����ֵ����Ϊ4.5 cm2
��6.5ʱ���ı���AB1C1D1�볤����ABCD�ص����ֵ����Ϊ4.5 cm2
��������
��1����ÿ�����Ƶ�A��ʱ����ת90��֮���ҵ���Ӧ�ĵ㣬Ȼ���������Ӹ��㼴�ɣ�
��2�����ص�����Ϊ�����Σ����ó����������ʽ���ɱ�ʾ��
�ڵ��߶�C1D1���߶�AD�����ʱ������еĴ���ʽ��ֵΪ4.5���г�һ������x�ķ��̣��ⷽ�̼���;
���߶�C1D1���߶�AD���Ҳ�ʱ���ȱ�ʾ���ص����ֵ�������������Ϊ4.5����Ӧx��ֵ.
��1����ͼ

��2�����ص�����Ϊ�����Σ����ݳ����������ʽ�ã�![]()
�ڵ��߶�C1D1���߶�AD�����ʱ, ![]() ���
���![]()
���߶�C1D1���߶�AD���Ҳ�ʱ, ![]()
��![]() ���
���![]()
���ϣ���![]() ��6.5ʱ���ı���AB1C1D1�볤����ABCD�ص����ֵ����Ϊ4.5 cm2
��6.5ʱ���ı���AB1C1D1�볤����ABCD�ص����ֵ����Ϊ4.5 cm2


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+2��ͼ���뷴��������y=��![]() ��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
��ͼ����A��B���㣬��x�ύ��D�㣬��C��D�������y��Գƣ�
��1����A��B��������ꣻ
��2������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪԭ�㣬A��BΪ���������㣬��A��ʾ����a����B��ʾ������b����![]() .
.
![]()
��1��a= ��b= ��
��2�����������Ƿ����һ��P��ʹ![]() �����У��������P��ʾ��������û�У���˵�����ɣ�
�����У��������P��ʾ��������û�У���˵�����ɣ�
��3����M�ӵ�A��������![]() ��·���˶�����·��
��·���˶�����·��![]() ���ٶ���ÿ��2����λ����·��
���ٶ���ÿ��2����λ����·��![]() �ϵ��ٶ���ÿ��4����λ��ͬʱ��N�ӵ�B������ÿ��3����λ�����յ�A�˶�������M��һ�λص���Aʱ�����˶�ֹͣ.�����MN=1��
�ϵ��ٶ���ÿ��4����λ��ͬʱ��N�ӵ�B������ÿ��3����λ�����յ�A�˶�������M��һ�λص���Aʱ�����˶�ֹͣ.�����MN=1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
(1)��12+3��(��2)3��(��6)��(��![]() )2��
)2��
(2)��2��12��(![]() )��
)��
(3)3x2+(2x2��3x)��(��x+5x2)��
(4)5(3a2b��ab2)��4(��ab2+3a2b)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ���Rt��ABC��ֱ�DZ�AC��б��AB�������ȱ���ACD���ȱ���ABE����֪��BAC=30�㣬EF��AB������ΪF������DF��
��1����˵��AC=EF��
��2����֤���ı���ADFE��ƽ���ı�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
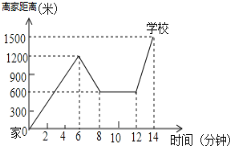
����Ŀ��������������ע�ⰲȫ����ͬѧ��������ѧ;��һ��Ҫע���ﳵ��ȫ��С���ﵥ����ѧ����������һ��ʱ������Ҫ��ij���飬�������ۻص��վ������»���꣬��������ȥѧУ�����������������õ�ʱ����·�̵Ĺ�ϵʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺
��1��С���ҵ�ѧУ��·���Ƕ����ף�
��2��С�������ͣ���˶��ٷ��ӣ�
��3��������ѧ;�У�С��һ����ʻ�˶����ף�һ�����˶��ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=CD��BF=DE��AE��BD��CF��BD������ֱ�ΪE��F��

��1����֤����ABE�ա�CDF��
��2����AC��BD���ڵ�O����֤��AO=CO��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ʾ������������Ϊ8cm��������һ���߳�Ϊ5cm�ĵȱ������Σ�
��1������������� ���⣬�� ���棻
��2��ͼ2���е�ͼ���Ǹ���������һ�ֱ���չ��ͼ��һ���֣��뽫����ȫ��һ�ּ�������
��3��Ҫ�����������ı�����ijЩ�������չ����һ��ƽ��ͼ�Σ���������� ���⣬���������ⳤ�ĺ͵����ֵΪ cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺![]()
��2����ͼ���ӳ��߶�AB��CʹBC��2AB���ӳ��߶�BA��DʹAD��3AB����E���߶�DB���е㣬��F���߶�AC���е㣬��AB��6cm����EF�ij��ȣ�
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com