

分析 (1)延长BA,CM交点N,先证明BC=BN,得出CN=2CE,再证明△BAF≌△CAN,得出对应边相等BF=CN,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,先证明PD=CD,得出PC=2CE,再证明△DNF≌△PNC,得出对应边相等DF=PC,即可得出结论.
解答 解:(1)如图(1),延长BA,CM交点N,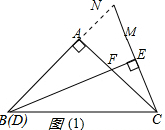
∵∠A=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM=$\frac{1}{2}$∠ABC=22.5°,
∴∠BCM=67.5°,
∴∠BNC=67.5°=∠BCM,
∴BC=BN,
∵BE⊥CE,
∴∠ABE=22.5°,CN=2CE,
∴∠ABE=∠ACM=22.5°,
在△BAF和△CAN中,$\left\{\begin{array}{l}{∠BAC=∠NAC=90°}\\{AB=AC}\\{∠ABF=∠ACM}\end{array}\right.$,
∴△BAF≌△CAN(ASA),
∴BF=CN,
∴BF=2CE;
(2)保持上述关系;DF=2CE;
证明如下:
作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
如图(2)所示:
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,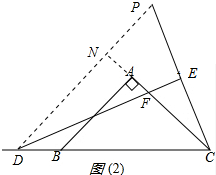
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中,$\left\{\begin{array}{l}{∠DNC=∠PNC}\\{ND=NC}\\{∠PDE=∠PCN}\end{array}\right.$,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质以及等腰三角形的判定与性质;通过作辅助线证明等腰三角形和全等三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买服装的套数 | 1套至49套 | 50套至99套 | 100套及以上 |
| 每套服装的价格 | 60元 | 55元 | 50元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com