
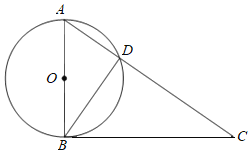
【题目】如图,AB是⊙O的直径,∠A=∠CBD.
(1)求证:BC是⊙O的切线.
(2)若∠C=35°,AB=6,求![]() 的长(结果保留π).
的长(结果保留π).
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由圆周角定理得出∠ADB=90°,得出∠A+∠ABD=90°,证得∠ABC=90°,即可得出BC是⊙O的切线.
(2)连接OD,可证得∠ABD=∠C=35°,由圆周角定理可得∠AOD=2∠ABD=70°,再通过弧长公式计算,即可得出答案.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠A=∠CBD,
∴∠CBD+∠ABD=90°,即∠ABC=90°,
∴BC⊥AB,
∴BC是⊙O的切线.
(2)解:连接OD,如图所示:
∵∠ABC=90°,
∴∠C+∠A=90°,
又∠A+∠ABD=90°,
∴∠ABD=∠C=35°,
∴∠AOD=2∠ABD=70°,
∵直径AB=6,
∴OA=3,
∴![]() 的长=
的长=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0).
(1)若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式.
(2)若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点(![]() ,0).
,0).
(3)设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
![]()
A.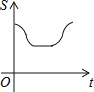 B.
B.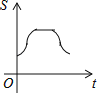
C.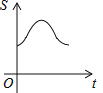 D.
D.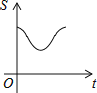
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C、A分别在x轴、y轴上,AB∥x轴,∠ACB=90°,反比例函数y=![]() (x>0)的图象经过AB的中点M.若点A(0,4)、C(2,0),则k的值为( )
(x>0)的图象经过AB的中点M.若点A(0,4)、C(2,0),则k的值为( )
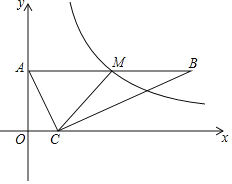
A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= (n为常数).
(n为常数).
(1)当n=1时,
①点P(﹣3,m)在此函数图象上,求m的值.
②当﹣4≤x≤3时,求此函数的最大值和最小值.
(2)当x<n时,若此函数的图象与坐标轴只有两个交点,求n的取值范围.
(3)若n>0,当此函数的图象与以A(0,3)、B(5,﹣2)、C(﹣5,﹣2)、D(﹣5,3)为顶点的四边形的边有且只有四个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,PA、PB是⊙O的切线,切点分别是点A、B
(1)如图1,若∠BAC=25°,求∠P的度数.
(2)如图2,若M是劣弧AB上一点,∠AMB=∠AOB,求∠P的度数.
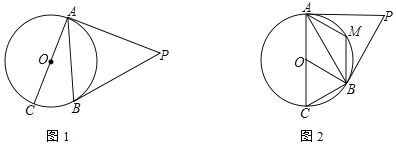
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,直线
,直线![]() 平行于
平行于![]() 轴,与抛物线另一个交点为
轴,与抛物线另一个交点为![]() .
.
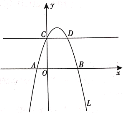
(1)求抛物线![]() 的函数表达式及点D的坐标;
的函数表达式及点D的坐标;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,
轴对称,![]() 是
是![]() 轴上的动点,在抛物线
轴上的动点,在抛物线![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点且
为顶点且![]() 为边的四边形是平行四边形,若存在,请求出点
为边的四边形是平行四边形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com