
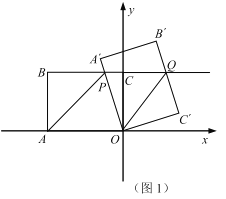
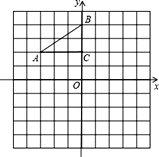
【题目】如图1,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 按顺时针方向旋转一定的角度
按顺时针方向旋转一定的角度![]() 得到矩形
得到矩形![]() ,此时边
,此时边![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() .
.
(1)连接![]() ,在旋转过程中,当
,在旋转过程中,当![]() 时,求点
时,求点![]() 坐标.
坐标.
(2)连接![]() ,当
,当![]() 时,若
时,若![]() 为线段
为线段![]() 中点,求
中点,求![]() 的面积.
的面积.
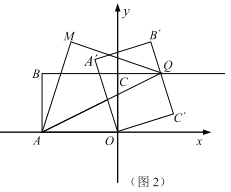
(3)如图2,连接![]() ,以
,以![]() 为斜边向上作等腰直角
为斜边向上作等腰直角![]() ,请直接写出在旋转过程中
,请直接写出在旋转过程中![]() 的最小值.
的最小值.
【答案】(1)P(﹣4,6);(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用∠PAO=∠POA得出PA=PO,进而得出AE=EO=4,即可得出P点坐标;
(2)首先得出Rt△OCQ≌Rt△OC'Q(HL),进而利用平行线的性质求出∠POQ=∠PQO,即可得出BP=PO,再利用勾股定理得出PQ的长,进而求出△OPQ的面积;
(3)先构造一组手拉手的相似三角形,将CM的长转化为![]() ,然后通过垂线段最短及全等三角形求解即可.
,然后通过垂线段最短及全等三角形求解即可.
解:如图1,过点P作PE⊥AO于点E,
∵![]() ,
,
∴AO=8,
∵∠PAO=∠POA
∴PA=PO,
∵PE⊥AO,
∴AE=EO=4,
∴P(﹣4,6);

(2)如图2,在Rt△OCQ和Rt△OC'Q中,
![]() ,
,
∴Rt△OCQ≌Rt△OC'Q(HL),
∴∠OQC=∠OQC',
又∵OP∥C'Q,
∵∠POQ=∠OQC',
∴∠POQ=∠PQO,
∴PO=PQ,
∵点P为BQ的中点,
∴BP=QP,
∴设BP=OP=x,
在Rt△OPC中,OP 2=PC 2+ OC 2,
∴x2=(8﹣x)2+62,
解得:x=![]() .
.
故S△OPQ=![]() ×CO×PQ=
×CO×PQ=![]() ×6×
×6×![]() =
=![]() .
.
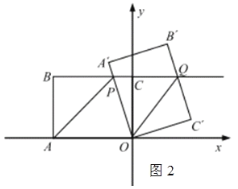
(3)如图3,连接CM、AC,在AC的右侧以AC为腰,∠ACG为直角作等腰直角三角形ACG,连接QG,

∵△AMQ与△ACG为等腰直角三角形,
∴![]() ,∠MAQ=∠CAG=45°,
,∠MAQ=∠CAG=45°,
∴![]() ,∠MAC=∠QAG
,∠MAC=∠QAG
∴△MAC∽△QAC,
∴![]() ,
,
∴![]() ,
,
∵点Q在直线BC上,
∴当GQ⊥BC时,GQ取得最小值,
如图3,作GH⊥BC,则GQ的最小值为线段GH的长,
∵∠ACG=∠B=90°,
∴∠ACB+∠GCH=∠ACB+∠BAC=90°,
∴∠GCH=∠BAC,
又∵∠B=∠GHC=90°,AC=CG,
∴△ABC≌△CHG(AAS)
∴GH=BC=8
∴GQ的最小值为8,
∴CM的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ABC=120°,AC=4,

(1)用直尺和圆规作出△ABC的外接圆⊙O(不写作法,保留作图痕迹);
(2)求∠AOC的度数;
(3)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
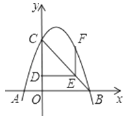
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
(1)求此抛物线的解析式;
(2)小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作O;②当点D与点O重合时,EF长度也可以看作O,于是他猜想:设点D运动到OC中点位置时,当线段EF最长,你认为他猜想是否正确,为什么?
(3)连接CF、DF,请直接写出△CDF为等腰三角形时所有t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD满足AB:BC=1: ![]() ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
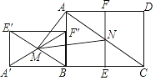
A. 4 ![]() B. 4 C. 2 D. 1
B. 4 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
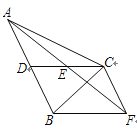
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com