
【题目】如图,∠D=∠B,补充下列条件之一,不一定能判定△ABC和△ADE相似的是( )
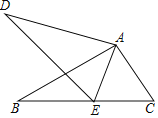
A.∠ACB=∠AEDB.∠CAE=∠BADC.∠BED=∠EACD.![]()
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
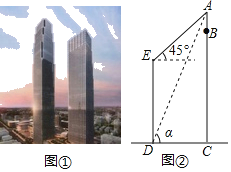
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AB=5cm,BC=7cm,S△ABC=14cm2,点P从点B出发,以3cm∕s的速度沿边BC向终点C运动,过点P作PQ⊥BC交折线BAC于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
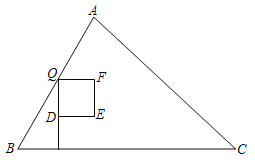
(1)∠C的度数为 ;
(2)当点P不与点C重合,且点F落在边AC上时x的值为 .
(3)当点P不与点B,C重合时,求y关于x的函数解析式;
(4)当直线BD平分△ABC的面积时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推进素质教育,在初一年级设立了六个课外兴趣小组,如图是六个兴趣小组的频数分布直方图和扇形统计图,请根据图中提供的信息回答下列问题:
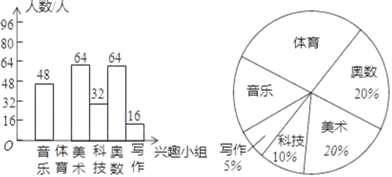
(1)初一年级共有多少人?
(2)补全频数分布直方图.
(3)求“从该年级中任选一名学生,是参加音乐、科技两个小组学生”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋中有大小、形状和质地等完全相同的4个小球,它们分别标有数字﹣1、﹣2、1、2.从袋中任意摸出一小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一小球.
(1)请你用列表或画树状图的方法表示摸出小球上的数字可能出现的所有结果;
(2)将第一次摸出的数字作为点的横坐标x,第二次摸出的数字作为点的纵坐标y,求点(x,y)落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
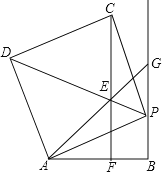
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
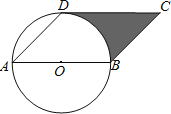
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为1,求图中阴影部分的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com