
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 为
为![]() 的中点,连结
的中点,连结![]() ,
,![]() .
.
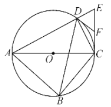
(1)求![]() 的度数.
的度数.
(2)求证:![]() 是
是![]() 的切线.
的切线.
(3)若![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)90°;(2)证明见解析;(3)![]() .
.
【解析】
(1)AC是直径,所以∠ADC=90°,所以∠CDE=90°;
(2)首先根据等腰三角形的性质得到∠DAO=∠ADO ,然后根据直角三角形斜边的中线的性质得到∠DEF=∠EDF,再根据∠DAO +∠DEF=90°,之后等量替换得到∠ODF=90°,从而证明DF是⊙O的切线;
(3)先证明△ADC∽△ACE,然后根据tan∠ABD=3可得tan∠ACD=3,设AD=3x,则CD=x,AC=![]() x,用相似三角形的性质可求出DE=
x,用相似三角形的性质可求出DE=![]() x,再求
x,再求![]() 即可.
即可.
解:(1)因为∠ADC是直径AC对应的圆周角,所以∠ADC=90°,所以∠CDE=90°.
(2)如图所示,连接OD,
因为OA=OD,所以△DAO是等腰三角形,则∠DAO=∠ADO,
由(1)得∠CDE=90°,所以△CDE是直角三角形,
又因为F是Rt△CDE斜边CE的中点,所以![]() ,
,
所以△DEF是等腰三角形,故∠DEF=∠EDF,
因为CE⊥AC,所以△ACE是直角三角形,
根据三角形内角和为180°,所以在Rt△ACE中∠DAO +∠DEF=90°,
因为∠DAO=∠ADO ,∠DEF=∠EDF ,
所以∠ODF=180°-(∠ADO+∠EDF)=180°-(∠DAO +∠DEF)=90°,
所以DF⊥OD,故DF是⊙O的切线;
(3)在△ADC和△ACE中,![]() ,
,
所以△ADC∽△ACE,根据相似三角形的性质,得![]() ,
,
因为tan∠ABD=3,所以tan∠ACD=3,
设AD=3x,则CD=x,∴AC=![]() x,
x,
所以![]() ,所以AE=
,所以AE=![]() x,DE=
x,DE=![]() x,
x,
所以![]() .
.


科目:初中数学 来源: 题型:
【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:
已知:如图,直线 l 和直线 l 外一点 A
求作:直线 AP,使得 AP∥l
作法:如图
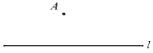
① 在直线 l 上任取一点 B,以点 A 为圆心,AB 为半径作圆,与直线 l 交于 B,C 两点.
② 连接 AC,AB,延长 BA 交⊙A 于点 D;
③ 作∠DAC 的平分线 AP,并反向延长.
所以直线 AP 就是所求作的直线
根据小星同学设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明
证明:∵AB=AC,
∴∠ABC=∠ACB( ① )(填推理的依据)
∵∠DAC 是△ABC 的外角,
∴∠DAC=∠ABC+∠ACB
∴∠DAC=2∠ABC
∵AP 平分∠DAC,
∴∠DAC=2∠DAP
∴ ②
∴AP∥l( ③ )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以![]() cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
(1)当P异于A.C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?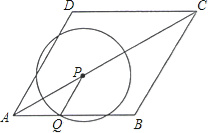
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
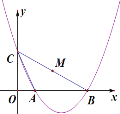
A. n=![]() (m-
(m-![]() )2-
)2-![]() B. n=
B. n=![]() (m-
(m-![]() )2+
)2+![]()
C. n=![]() (m-
(m-![]() )2-
)2-![]() D. n=
D. n=![]() (m-
(m-![]() )2-
)2-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一个含有45角的三角板的其中一个锐角顶点置于点A(﹣3,﹣3)处,将其绕点A旋转,这个45角的两边所在的直线分别交x轴,y轴的正半轴于点B,C,连结BC,函数y=![]() (x>0)的图象经过BC的中点D,则( )
(x>0)的图象经过BC的中点D,则( )
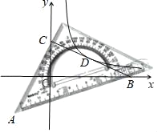
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BDcos∠HBD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732,![]() =1.414)
=1.414)
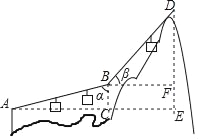
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com