
【题目】如图, ![]() 为等边三形内的一点,
为等边三形内的一点, ![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转60°得到线段
为旋转中心逆时针旋转60°得到线段![]() ,下列结论:①点
,下列结论:①点![]() 与点
与点![]() 的距离为5;②
的距离为5;②![]() ;③
;③![]() 可以由
可以由![]() 绕点
绕点![]() 进时针旋转60°得到;④点
进时针旋转60°得到;④点![]() 到
到![]() 的距离为3;⑤
的距离为3;⑤![]() ,其中正确的有( )
,其中正确的有( )
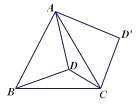
A.2个B.3个C.4个D.5个
【答案】B
【解析】
连结DD′,根据旋转的性质得AD=AD′,∠DAD′=60°,可判断△ADD′为等边三角形,则DD′=5,可对①进行判断;由△ABC为等边三角形得到AB=AC,∠BAC=60°,则把△ABD逆时针旋转60°后,AB与AC重合,AD与AD′重合,于是可对③进行判断;再根据勾股定理的逆定理得到△DD′C为直角三角形,则可对②④进行判断;由于S四边形ADCD′=S△ADD′+S△D′DC,利用等边三角形的面积公式和直角三角形面积公式计算后可对⑤进行判断.
解:连结DD′,如图,
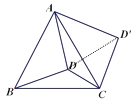
∵线段AD以点A为旋转中心逆时针旋转60°得到线段AD′,
∴AD=AD′,∠DAD′=60°,
∴△ADD′为等边三角形,
∴DD′=5,所以①正确;
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∴把△ABD逆时针旋转60°后,AB与AC重合,AD与AD′重合,
∴△ACD′可以由△ABD绕点A逆时针旋转60°得到,所以③正确;
∴D′C=DB=4,
∵DC=3,
在△DD′C中,∵32+42=52,
∴DC2+D′C2=DD′2,
∴△DD′C为直角三角形,
∴∠DCD′=90°,
∵△ADD′为等边三角形,
∴∠ADD′=60°,
∴∠ADC≠150°,所以②错误;
∵∠DCD′=90°,
∴DC⊥CD′,
∴点D到CD′的距离为3,所以④正确;
∵S四边形ADCD′=S△ADD′+S△D′DC=![]() ,所以⑤错误.
,所以⑤错误.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,
,![]() 为图形内一点,连接
为图形内一点,连接![]() ,
,![]() .
.
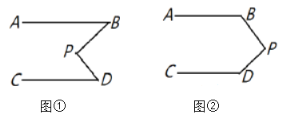
(1)如图①,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论;
之间的等量关系,并证明你的结论;
(2)如图②,请直接写出![]() ,
,![]() ,
,![]() 之间的关系式;
之间的关系式;
(3)你还能就本题作出什么新的猜想?请画图并写出你的结论(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
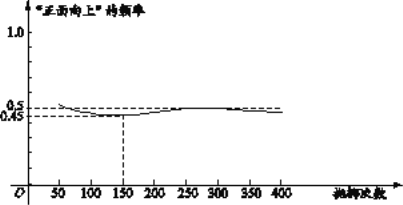
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动鞋经销商随机调查某校40名女生的运动鞋号码,结果如下表:
鞋的号码 | 35.5 | 36 | 36.5 | 37 | 37.5 |
人数 | 4 | 6 | 16 | 12 | 2 |
现在该经销商要进200双上述五种女运动鞋,你认为应该怎样进货比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
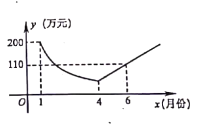
A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com