
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1,дке§ЗНаЮABCDжа,ЕуE,FЗжБ№дкБпBC,CDЩЯ,AE,BFНЛгкЕуO,ЁЯAOFЃН90Ёу.
ЧѓжЄЃКBFЃНAE.

(2) ШчЭМ2,е§ЗНаЮABCDБпГЄЮЊ12ЃЌНЋе§ЗНаЮбиMNелЕўЃЌЪЙЕуAТфдкDCБпЩЯЕФЕуEДІЃЌЧвDE=5ЃЌЧѓелКлMNЕФГЄЁЃ

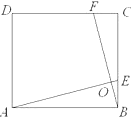
(3) вбжЊЕуE,H,F,GЗжБ№дкОиаЮABCDЕФБпAB,BC,CD,DAЩЯЃЌEF,GHНЛгкЕуO,
ЁЯFOHЃН90Ёу,EFЃН4. жБНгаДГіЯТСаСНЬтЕФД№АИЃК
ЂйШчЭМ3,ОиаЮABCDгЩ2ИіШЋЕШЕФе§ЗНаЮзщГЩ,дђ GH=___________ЃЛ
ЂкШчЭМ4,ОиаЮABCDгЩnИіШЋЕШЕФе§ЗНаЮзщГЩ,дђ GH=___________ЃЛ(гУnЕФДњЪ§ЪНБэЪО).

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЈ2ЃЉ13ЃЈ3ЃЉ8ЃЌ 4n
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОне§ЗНаЮЕФаджЪПЩЕУAB=BCЃЌЁЯABC=ЁЯBCD=90ЁуЃЌдйИљОнЭЌНЧЕФгрНЧЯрЕШЧѓГіЁЯEAB=ЁЯFBCЃЌШЛКѓРћгУЁАНЧБпНЧЁБжЄУїЁїABEКЭЁїBCFШЋЕШЃЌдйИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШжЄУїМДПЩЃЛ
ЃЈ2ЃЉСЌНгAEЃЌЙ§ЕуNзїNHЁЭADгкHЃЌИљОнЗелЕФаджЪПЩЕУAEЁЭNMЃЌШЛКѓЧѓГіЁЯDAE=ЁЯMNHЃЌдйРћгУЁАНЧБпНЧЁБжЄУїЁїADEКЭЁїNHMШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУAE=MNЃЌШЛКѓРћгУЙДЙЩЖЈРэСаЪНЧѓГіAEЃЌДгЖјЕУНтЃЛ
ЃЈ3ЃЉЙ§ЕуFзїFMЁЭABгкMЃЌЙ§ЕуGзїGNЁЭBCгкNЃЌРћгУЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЧѓНтМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉжЄУїЃКШчЭМЃЌЁпЫФБпаЮABCDЮЊе§ЗНаЮЃЌ
ЁрAB=BCЃЌЁЯABC=ЁЯBCD=90Ёу
ЁрЁЯ EAB+ЁЯAEB=90ЁуЃЎ
ЁпЁЯEOB=ЁЯAOF=90ЁуЃЌЁрЁЯFBC+ЁЯAEB=90ЁуЃЌ
ЁрЁЯEAB=ЁЯFBC
ЁрЁїABEЁеЁїBCFЃЌЁрAE = BF
(2)СЌНсAE,Й§ЕуNзїNHЁЭAD,жЄУїЁїMNHЁеEAD
ЁрMN=AE
гЩЙДЙЩЖЈРэЕУAE=13, ЁрMN=13
ЃЈ3ЃЉ8ЃЎ 4n



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуPЕФзјБъЮЊЃЈ2ЉaЃЌ3a+6ЃЉЃЌЧвЕуPЕНСНзјБъжсЕФОрРыЯрЕШЃЌдђa=_____
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЗНГЬЪЧвЛдЊвЛДЮЗНГЬЕФЪЧЃЈ ЃЉ
A. S=ab B. 2+5=7 C. 4x +1=x+2 D. 3x+2y=6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕБmЪБЃЌКЏЪ§y=ЃЈmЉ2ЃЉx2+3xЉ5ЃЈmЮЊГЃЪ§ЃЉЪЧЙигкxЕФЖўДЮКЏЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЙигкЕШБпШ§НЧаЮЕФУшЪіДэЮѓЕФЪЧЃЈ ЃЉ
A.Ш§БпЯрЕШЕФШ§НЧаЮЪЧЕШБпШ§НЧаЮ
B.Ш§ИіНЧЯрЕШЕФШ§НЧаЮЪЧЕШБпШ§НЧаЮ
C.гавЛИіНЧЪЧ60ЁуЕФШ§НЧаЮЪЧЕШБпШ§НЧаЮ
D.гаСНИіНЧЪЧ60ЁуЕФШ§НЧаЮЪЧЕШБпШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊСНИіБфСПxЃЌyжЎМфЕФЙиЯЕЪНЮЊy=ЃЈaЉ2ЃЉx2+ЃЈb+2ЃЉxЉ3ЃЎ
ЃЈ1ЃЉЕБЪБЃЌxЃЌyжЎМфЪЧЖўДЮКЏЪ§ЙиЯЕЃЛ
ЃЈ2ЃЉЕБЪБЃЌxЃЌyжЎМфЪЧвЛДЮКЏЪ§ЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.вЛзщЖдБпЦНааЕФЫФБпаЮЪЧЬнаЮ
B.гаСНИіНЧЪЧжБНЧЕФЫФБпаЮЪЧжБНЧЬнаЮ
C.жЛгаЯрСкЕФСНИіНЧЪЧжБНЧЕФЫФБпаЮЪЧжБНЧЬнаЮ
D.вЛзщЖдБпЦНааСэвЛзщЖдБпЯрЕШЕФЫФБпаЮЪЧЕШбќЬнаЮ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com