
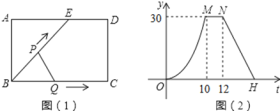
【题目】如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿![]() 运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是
运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是![]() ,设P,Q出发t秒时,
,设P,Q出发t秒时,![]() 的面积为
的面积为![]() ,已知y与t的函数关系的图象如图
,已知y与t的函数关系的图象如图![]() 曲线OM为抛物线的一部分
曲线OM为抛物线的一部分![]() ,则下列结论:
,则下列结论:![]() ;
;![]() 直线NH的解析式为
直线NH的解析式为![]() ;
;![]() 不可能与
不可能与![]() 相似;
相似;![]() 当
当![]() 时,
时,![]() 秒.其中正确的结论个数是( )
秒.其中正确的结论个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,即可判断①,再根据M、N是从10秒到12秒,可得ED的长度,, 当点P运动到点C时,面积变为0,可求得点H的坐标,求出解析式,即可判断②,当△ABE与△QBP相似时,点P在DC上,求出PQ的长,即可判断③,t=13时,PQ=5,此时tan∠PBQ=![]() =
=![]() ,即可判断④.
,即可判断④.
解:①据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=10cm,S△BCE= ![]() BC·AB=30,
BC·AB=30,
∴AB=6,故①正确;
②根据1012秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=18,
故点H的坐标为(18,0),
设直线NH的解析式为y=kx+b,
将点H(18,0),点N(12,30)代入可得:![]() ,
,
解得:![]() .
.
故直线NH的解析式为:y=5t+90,故②正确;
③当△ABE与△QBP相似时,点P在DC上,如图2所示:
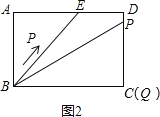
∵tan∠PBQ=tan∠ABE=![]() ,
,
∴![]() ,
,
∵BQ=10,
∴PQ=7.5,
∴PQ>CD,
∴△ABE与△QBP不可能相似,故③正确;
④t=13时,PQ=18-13=5,
此时tan∠PBQ=![]() =
=![]() ,
,
∴∠PBQ≠30,故④错误,
综上可得①②③正确,共3个.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,一张半径为![]() 的圆形纸片,点
的圆形纸片,点![]() 为圆心,将该圆形纸片沿直线
为圆心,将该圆形纸片沿直线![]() 折叠,直线
折叠,直线![]() 交
交![]() 于
于![]() 两点.
两点.
(1)若折叠后的圆弧恰好经过点![]() ,利用直尺和圆规在图中作出满足条件的一条直线
,利用直尺和圆规在图中作出满足条件的一条直线![]() (不写作法,保留作图痕迹),并求此时线段
(不写作法,保留作图痕迹),并求此时线段![]() 的长度.
的长度.
(2)已知![]() 是
是![]() 一点,
一点,![]() .
.
①若折叠后的圆弧经过点![]() ,则线段
,则线段![]() 长度的取值范围是________.
长度的取值范围是________.
②若折叠后的圆弧与直线![]() 相切于点
相切于点![]() ,则线段
,则线段![]() 的长度为_________
的长度为_________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解该校初三学生居家学习期间参加“网络自习室”自主学习的情况,随机抽查了部分学生在两周内参加“网络自习室”自主学习的天数,并用得到的数据绘制了如下两幅不完整的统计图.
请根据图中提供的信息,回答下列问题.
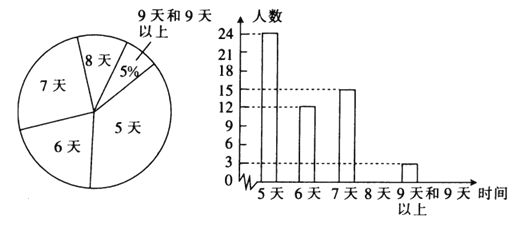
(1)补全条形统计图.
(2)部分学生在两周内参加“网络自习室”自主学习天数的众数为______,中位数为________;
(3)如果该校初三年级约有![]() 名学生,请你估计在这两周内全校初三年级可能有多少名学生参加“网络自习室”自主学习的天数不少于
名学生,请你估计在这两周内全校初三年级可能有多少名学生参加“网络自习室”自主学习的天数不少于![]() 天.
天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜市场为指导某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供的信息如下:
信息1:售价和月份满足一次函数关系,如下表所示.
月份 | … | 3 | 6 | … |
售价 | … | 5 | 3 | … |
信息2:成本和月份满足二次函数关系,并且知道该种蔬菜在6月成本达到最低为1元/千克,9月成本为4元/千克.
根据以上信息回答下列问题:
(1)在7月,这种蔬菜的成本是多少元每千克?
(2)在过去的一年中,某商家平均每天卖出![]() 该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数 y=f(x)满足:对于自变量 x 的取值范围内的任意 x1,x2,
(1)若 x1<x2,都有 f(x1)<f(x2),则称 f(x)是增函数;
(2)若 x1<x2,都有 f(x1)>f(x2),则称 f(x)是减函数.
例题:证明函数f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
证明:设 0<x1<x2,
f(x1)﹣f(x2)=![]() .
.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴![]() >0.即 f(x1)﹣f(x2)>0.
>0.即 f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数 f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数![]() .
.
f(﹣1)=![]() +(﹣2)=-1,f(﹣2)=
+(﹣2)=-1,f(﹣2)=![]() +(﹣4)=
+(﹣4)=![]() .
.
(1)计算:f(﹣3)= ,f(﹣4)= ;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
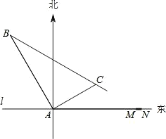
【题目】在某飞机场东西方向的地面 l 上有一长为 1km 的飞机跑道 MN(如图),在跑道 MN的正西端 14.5 千米处有一观察站 A.某时刻测得一架匀速直线降落的飞机位于点 A 的北偏西30°,且与点 A 相距 15 千米的 B 处;经过 1 分钟,又测得该飞机位于点 A 的北偏东 60°,且与点 A 相距 5![]() 千米的 C 处.
千米的 C 处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道 MN 之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在每个小正方形的边长为1的网格中,△ABC的顶点A、B、C均在格点上,点D为AC边上的一点.
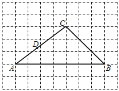
(1)线段AC的长为 .
(2)在如图所示的网格中,AM是△ABC的角平分线,在AM上求一点P,使CP+DP的值最小,请用无刻度的直尺,画出AM和点P,并简要说明AM和点P的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块宣传牌![]() .小明在山坡的坡脚
.小明在山坡的坡脚![]() 处测得宣传牌底部
处测得宣传牌底部![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处测得宣传牌顶部
处测得宣传牌顶部![]() 的仰角为
的仰角为![]() .已知山坡
.已知山坡![]() 的坡度
的坡度![]() ,
,![]() 米,
米,![]() 米.
米.
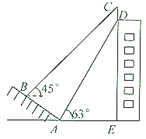
(1)求点![]() 距地面的高度;
距地面的高度;
(2)求大楼![]() 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com