
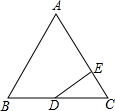
 如图,△ABC是等边三角形,D为BC边的中点,DE⊥AC于点E.试探索线段CE与线段AC的数量关系,并说明理由.
如图,△ABC是等边三角形,D为BC边的中点,DE⊥AC于点E.试探索线段CE与线段AC的数量关系,并说明理由. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
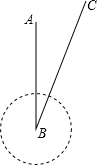 据气象观测,某台风中心正位于城市A正南方向220km的B处,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现以15km/h的速度沿北偏东30°的BC方向移动,且台风中心风力不变,若城市所受风力达到或超过4级,则会受台风影响.
据气象观测,某台风中心正位于城市A正南方向220km的B处,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现以15km/h的速度沿北偏东30°的BC方向移动,且台风中心风力不变,若城市所受风力达到或超过4级,则会受台风影响.查看答案和解析>>
科目:初中数学 来源: 题型:
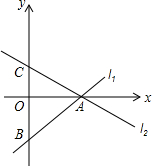 如右图,两直线l1:y=kx-2b+1和l2:y=(1-k)x+b-1交于x轴上一点A,与y轴分别交于点B、C,若A的横坐标为2,
如右图,两直线l1:y=kx-2b+1和l2:y=(1-k)x+b-1交于x轴上一点A,与y轴分别交于点B、C,若A的横坐标为2,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com