
��ͼ2 - 64��ʾ����ƽ��ֱ������ϵ�У������ߵĶ���P��x��ľ�����4����������x���ཻ��O��M���㣬OM��4������ABCD�ı�BC���߶�OM�ϣ���A��D���������ϣ�
(1)��д��P��M��������꣬�������������ߵĽ���ʽ��
(2)�����ABCD���ܳ�Ϊl����l�����ֵ��
(3)����OP��PM�����PMOΪ���������Σ����ж������������Ƿ��ڵ�Q(����M��)��ʹ�á�OPQҲ�ǵ���������(�������Q�������)����Ҫ ˵��������ɣ�
˵��������ɣ�

�⣺(1)������֪��P������Ϊ(2��4)����M������Ϊ(4��0)���ʿ��������ߵĽ���ʽΪy��a(x��2) 2+4����Ϊ�������߾�����M(4��0)������0��a(4��2)2 +4�����a=��l�����������ߵĽ���ʽΪy=��(x��2)2+4����x2+4x�� (2)��A�������ΪA(x��y)������2<x<4����AD��BC=2x��4��AB=CD��y�����ε��ܳ�l=2(AB+AD)��2(y+2x��4)=2(��x2+4x+2x��4)=��2x2+12x��8=��2(x��3) 2+10����Ϊ2<3<4�����Ե�x=3ʱ�����ε��ܳ�l ������ֵΪ10��
������ֵΪ10��  (3)���ڣ��������£���
(3)���ڣ��������£��� ����ɵ�OM��4��OP=PM=2
����ɵ�OM��4��OP=PM=2 ,��OM��PM����O
,��OM��PM����O P�Ĵ�ֱƽ����һ�������������ཻ���ҽ��㼴ΪQ�㣮
P�Ĵ�ֱƽ����һ�������������ཻ���ҽ��㼴ΪQ�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊ�˽���ѧ����ȡ��Ѷ����Ҫ���������á�A����ֽ��B�����ӣ�C�����磬D�����ߵ��ˣ�E�����������ѡ��(�����б�ѡ��ֻ��ѡһ��)�ĵ����ʾ����������ȡ50����ѧ�����и��ʾ����飬���ݵ���Ľ����������ͼ��ͼ���õ���ķ�ʽ�� ��ͼ�е�a��ֵ��( )
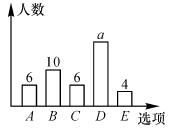
A.ȫ����飬26 B.ȫ����飬24
C.�������飬26 D.�������飬24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵���д������( )
A ���ں���y����x2�У���x��0ʱy�����ֵ0
B���ں���y��2x2�У���x��0ʱy��x�����������
C��������y��2x2��y����x2�� �У�������y��2x2�Ŀ�����С��������y����x2�Ŀ������
�У�������y��2x2�Ŀ�����С��������y����x2�Ŀ������
D������a���������Ǹ�����������y��ax2�Ķ��㶼������ԭ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���κ��� y=2��x��3��2+5��ͼ��Ŀ��ڷ��Գ���Ͷ�������ֱ�Ϊ�� ��
A���������£��Գ���x=��3����������Ϊ��3,5��
B���������£��Գ���x��3����������Ϊ��3��5��
C���������ϣ��Գ���x=��3����������Ϊ(��3,5)
D���������ϣ��Գ���x=��3����������Ϊ(��3,��5��
�鿴�𰸺ͽ���>>
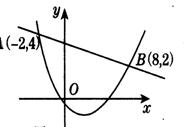
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪���κ���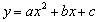 (a��0����һ�κ���y=kx
(a��0����һ�κ���y=kx +m(k��0����ͼ���ཻ�ڵ�A����2��4��,B(8��2)����ͼ��ʾ����ʹy1��y2������xȡֵ��Χ��_______
+m(k��0����ͼ���ཻ�ڵ�A����2��4��,B(8��2)����ͼ��ʾ����ʹy1��y2������xȡֵ��Χ��_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������y��2(x��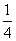 )2��
)2��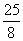 �Ķ��������� ���Գ����� ����x��Ľ����� ����y��Ľ����� ��
�Ķ��������� ���Գ����� ����x��Ľ����� ����y��Ľ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��������y��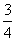 (x+5)2��6����ƽ��4����λ��������ƽ��5����λ�����ʱ�����ߵĽ���ʽ��
(x+5)2��6����ƽ��4����λ��������ƽ��5����λ�����ʱ�����ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
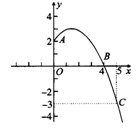
��֪������y=ax2+bx+c����A��B��C���㣬��x��0ʱ����ͼ����ͼ��ʾ��
��1���������ߵĽ���ʽ��д�������ߵĶ������ꣻ
��2������������y=ax2+bx+c��x<0ʱ��ͼ��
��3������������y=ax2+bx+c��д��xΪ��ֵʱ��y>0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
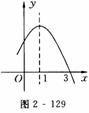 ��֪���κ���y����x2��2x��m�IJ���ͼ����ͼ 2��129��ʾ�������x��һԪ���η��̣�x2��2x��m��0�Ľ�Ϊ ��
��֪���κ���y����x2��2x��m�IJ���ͼ����ͼ 2��129��ʾ�������x��һԪ���η��̣�x2��2x��m��0�Ľ�Ϊ ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com