
 ��ͼ����֪�����ߵĶ���ΪM��2��-4�����ҹ���A��-1��5��������AM��x���ڵ�B��
��ͼ����֪�����ߵĶ���ΪM��2��-4�����ҹ���A��-1��5��������AM��x���ڵ�B������ ��1�����������߹�����M��2��-4����A��-1��5�����㣬�ö���ʽ����ϵ��������������κ����Ľ���ʽ��
��2�����P��x��y����Q�������ǣ�2x��0������2x����ֱ��AM�Ľ���ʽ���Ϳ������R�����꣮�õ�QR�ij��ȣ�QR���ϵĸ���x�������QRP������Ϳ�����x��ʾ�������õ�S��x�ĺ�������ʽ��
��3��ʹS��PQR=2����s=2���뺯���Ľ���ʽ���Ϳ��Եõ�����x�ķ��̣��ⷽ�����Ϳ��ԣ�
��4�����������Ե�N��B��Q��ɵ����������PQO���ƣ������������������ʺ��ɶ��������������N�����꣮
��� �⣨1���������ߵĶ���ΪM��2��-4����
���������߽���ʽΪy=a��x-2��2-4��
�������߹���A��-1��5����
��5=a��-1-2��2-4��
��ã�a=1��
�������ߵĽ���ʽ��y=��x-2��2-4��
�����������ߵĽ���ʽΪy=x2-4x��
��2����ֱ��AM����ʽ��y=kx+b��
��M��2��-4����A��-1��5����
��$\left\{\begin{array}{l}{-4=2k+b}\\{5=-1k+b}\end{array}\right.$
��ã�k=-3��b=2��
��ֱ��AM����ʽ��y=-3x+2��
��y=0��x=$\frac{2}{3}$��
��B��$\frac{2}{3}$��0����
��P��x��y������������x���·������� M��һ���ϵĶ��㣬
��0��x��$\frac{1}{3}$ʱ��
��P��x��x2-4x����
����PO��PQΪ���ĵ��������ε���һ����Q��x���ϣ�
��Q�������ǣ�2x��0����
��QR��x�ᣬ
��R��2x��-6x+2����
��QR=|-6x+2|=-6x+2��PR=2x-x=x��
��S��QPR=$\frac{1}{2}$����-6x+2����x=-3x2+x��
��$\frac{1}{3}$��x��2ʱ��
��P��x��x2-4x����
����PO��PQΪ���ĵ��������ε���һ����Q��x���ϣ�
��Q�������ǣ�2x��0����
��QR��x�ᣬ
��R��2x��-6x+2����
��QR=|-6x+2|=6x-2��PR=2x-x=x��
��S��QPR=$\frac{1}{2}$����6x-2����x=3x2-x��
��S=$\left\{\begin{array}{l}{y=-3{x}^{2}+x\\;0��x��\frac{1}{3}}\\{y=3{x}^{2}-x\\;\frac{1}{3}��x��2}\end{array}\right.$��
��3�����ڣ�
-3x2+x=2�������ã�3x2-x+2=0��
��=1-24��0��
�����⣻
3x2-x=2�������ã�3x2-x-2=0��
��ã�x=1����x=-$\frac{2}{3}$���ᣩ��
��x=1�����P��
��P��1��-3����
����ڵ�P��1��-3����ʹS��PQR=2��
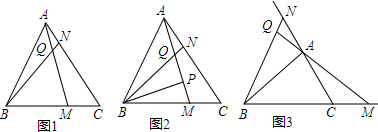
��4������PQO�ס�NQBʱ������ͼ��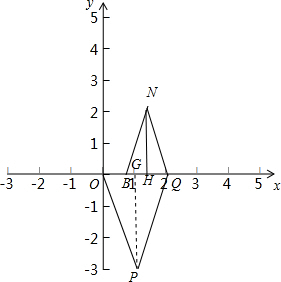
�ֱ����N��P��x�ᴹ�ߣ�����ΪH��G��
PQ=$\sqrt{10}$��OQ=2��BQ=$\frac{4}{3}$��PG=3��BH=$\frac{2}{3}$��OH=$\frac{4}{3}$��
��$\frac{OQ}{BQ}=\frac{PG}{NH}$��
���NH=2��
��N��$\frac{4}{3}$��2����
����PQO�ס�BQNʱ������ͼ��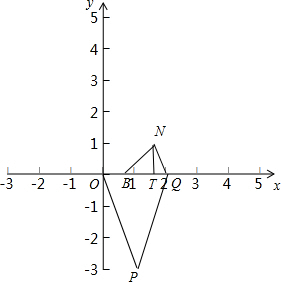
����N��x�ᴹ�ߣ�����ΪT��
PQ=$\sqrt{10}$��OQ=2��BQ=$\frac{4}{3}$��BN=$\frac{4}{3}$��
$\frac{PQ}{BQ}=\frac{OQ}{NQ}$
��ã�NQ=$\frac{4\sqrt{10}}{15}$��
��BT=x��TQ=$\frac{4}{3}$-x��
��BN2-BT2=NQ2-TQ2
��$\frac{16}{9}$-x2=��$\frac{4\sqrt{10}}{15}$��2-��$\frac{4}{3}$-x��2��
��ã�x=$\frac{16}{15}$��
��NT=BN2-BT2=$\frac{4}{5}$��
0T=$\frac{16}{15}$+$\frac{2}{3}$=$\frac{26}{15}$��
��N��$\frac{26}{15}$��$\frac{4}{5}$����
����PQO�ס�QNBʱ������ͼ��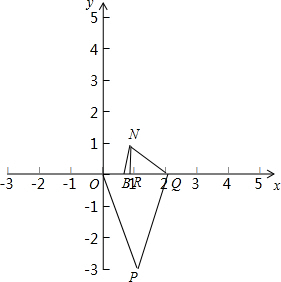
����N��x�ᴹ�ߣ�����ΪR��
PQ=$\sqrt{10}$��OQ=2��BQ=$\frac{4}{3}$��QN=$\frac{4}{3}$��
$\frac{PQ}{BQ}=\frac{OQ}{BN}$��
��ã�NB=$\frac{4\sqrt{10}}{15}$��
��BR=x��RQ=$\frac{4}{3}$-x��
��BN2-BR2=NQ2-RQ2
��ã�x=$\frac{4}{15}$��
��BR=BN2-NR2=$\frac{4}{5}$��
0R=$\frac{4}{15}$+$\frac{2}{3}$=$\frac{14}{15}$��
��N��$\frac{14}{15}$��$\frac{4}{5}$����
����������N����������$\frac{4}{3}$��2������$\frac{26}{15}$��$\frac{4}{5}$������$\frac{14}{15}$��$\frac{4}{5}$����
���� ��Ŀ�����˴���ϵ���������Ľ���ʽ���Լ�����ϵ�������ε�����������߶εij�������һ��Ҫת��Ϊ����ͼ���ϵĵ����������⣮�������������ε��������ⲻҪ����©��������Ŀ������ѣ��ʺ�ѧ�������п�ѹ��ѵ����


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com