
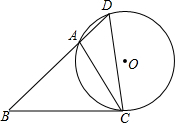
 如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆
如图,在△ABC中,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆| 2 |
| 2 |
 ∵CE是⊙O的直径,
∵CE是⊙O的直径,| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 82+42 |
| 5 |
| AC |
| CE |
| AF |
| CF |
| 8 |
| 4 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
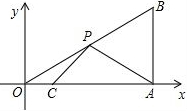 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,其中点B的坐标为(4,3),点C和点P分别为直角边OA、斜边OB上的动点,则PA+PC的最小值为查看答案和解析>>
科目:初中数学 来源: 题型:
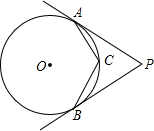 如图,PA,PB分别与⊙O相切于A,B两点,点C是劣弧AB上一动点(不与A,B重合),∠P=70°,则∠C=( )
如图,PA,PB分别与⊙O相切于A,B两点,点C是劣弧AB上一动点(不与A,B重合),∠P=70°,则∠C=( )| A、110° | B、115° |
| C、120° | D、125° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 “宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60):
“宿松家乐福超市”以每件20元的价格进购一批商品,试销一阶段后发现,该商品每天的销售量y(件)与售价x(元/件)之间的函数关系如图(20≤x≤60):查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,∠1=15°12′,OA⊥OC,点B、O、D在同一直线上,则∠2的度数为( )
如图,∠1=15°12′,OA⊥OC,点B、O、D在同一直线上,则∠2的度数为( )| A、105.12° |
| B、105.2° |
| C、74.8° |
| D、164.8° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com